题目内容
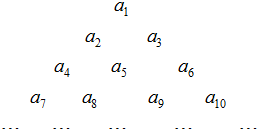 已知等差数列{an}中,a3=5,a6=14,将此等差数列的各项排成如图三角形数阵:则此数阵中第30行从左到右的第10个数是( )
已知等差数列{an}中,a3=5,a6=14,将此等差数列的各项排成如图三角形数阵:则此数阵中第30行从左到右的第10个数是( )分析:设等差数列的公差为d,利用等差数列的通项公式可得an.此数阵中前第29行共有1+2+…+29=
=435.因此此数阵中第30行从左到右的第10个数是第445个数,求出a445即可.
| 29×30 |
| 2 |
解答:解:设等差数列的公差为d,∵a3=5,a6=14,∴
,解得
.
∴an=-1+3(n-1)=3n-4.
此数阵中前第29行共有1+2+…+29=
=435.
∴此数阵中第30行从左到右的第10个数是第445个数,
∴a445=3×445-4=1331.
故选A.
|
|
∴an=-1+3(n-1)=3n-4.
此数阵中前第29行共有1+2+…+29=
| 29×30 |
| 2 |
∴此数阵中第30行从左到右的第10个数是第445个数,
∴a445=3×445-4=1331.
故选A.
点评:本题考查了等差数列的通项公式和前n项和公式,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.