题目内容

14．已知P为单位圆上任一点，若存在定点M，使得直线PM的斜率取值范围为[0，$\sqrt{3}$]，则该定点M的坐标为（-$\sqrt{3}$，-1）．

分析 根据题意，画出图形，结合图形求出点M的坐标．

解答 解：根据题意，画出图形，如图所示；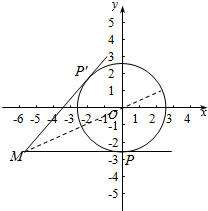

∵kPM=0，kP′M=$\sqrt{3}$，连接OP，则kOP=$\frac{\sqrt{3}}{3}$；
∴直线PM的方程为y=-1，
直线OM的方程为y=$\frac{\sqrt{3}}{3}$x；
由$\left\{\begin{array}{l}{y=-1}\\{y=\frac{\sqrt{3}}{3}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-1}\end{array}\right.$，
∴点M（-$\sqrt{3}$，-1）；
即存在定点M，使得直线PM的斜率取值范围为[0，$\sqrt{3}$]，
故答案为：（-$\sqrt{3}$，-1）．

点评 本题考查了直线与圆的应用问题，解题的关键是根据图形得出定点M的位置，是基础题目．

练习册系列答案
相关题目
4．若A、B、C是三个集合，则“A∩B=C∩B”是“A=C”（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件
5．已知函数$y=4sin（2x+\frac{π}{6}）（0≤x≤\frac{7π}{6}）$的图象与一条平行于x轴的直线有三个交点，其横坐标分别为x1，x2，x3（x1＜x2＜x3），则x1+2x2+x3=$\frac{5π}{3}$．
2．已知函数f（x）=x2+2bx+c为偶函数，关于x的方程f（x）=a（x+1）2的解构成集合{l}．
（1）求a、b、c的值．
（2）若x∈[-2，2]，求证：$\sqrt{f（x）}≤\frac{\sqrt{5}-1}{2}|x|+1$；
（3）设g（x）=$\sqrt{f（x）}+\sqrt{f（2-x）}$，若存在实数x1，x2∈[0，2]使得|g（x1）-g（x2）|≥m，求实数m的取值范围．
9．已知抛物线上一点A（2，1）到焦点的距离为2．
（1）求抛物线的方程；
（2）过点Q（0，-2）任作一动直线交抛物线于M、N两点，记$\overrightarrow{QM}$=$λ\overrightarrow{NQ}$，若在直线上取一点R，使得$\overrightarrow{RM}$=$-λ\overrightarrow{NR}$，试判断当直线运动时，点R是否在某一轨迹上运动，若是，求出该轨迹的方程；若不是，请说明理由．
19．已知数列{an}满足a1=2，an+1=an+$\frac{1}{{n}^{2}+n}$，求an．
6．已知一组函数fn（x）=sinnx+cosnx，x$∈[0，\frac{π}{2}$]，n∈N*，则下列说法正确的是（1）（2）（4）
（1）?n∈N*，fn（x）≤$\sqrt{2}$恒成立．
（2）f4（x）在[0，$\frac{π}{4}$]上单调递减，在[$\frac{π}{4}$，$\frac{π}{2}$]上单调递增．
（3）n为大于1的奇函数时，fn（x）的最小正周期为π．
（4）n为大于2的偶函数时，fn（x）的值域为[（$\frac{1}{2}$）${\;}^{\frac{n}{2}-1}$，1]．
3．$\frac{2sin10°+sin50°}{cos50°}$的值为$\sqrt{3}$．
4．若存在x∈[2，3]，使不等式$\frac{1+ax}{x•{2}^{x}}$≥1成立，则实数a的最小值为$\frac{7}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网