题目内容
已知函数![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 的“不动点”;若
的“不动点”;若![]() ,则称
,则称![]() 为
为![]() 的“稳定点”。记集合
的“稳定点”。记集合![]()
(1)已知![]() ,若
,若![]() 是在
是在![]() 上单调递增函数,是否有
上单调递增函数,是否有![]() ?若是,请证明。
?若是,请证明。
(2)记![]() 表示集合
表示集合![]() 中元素的个数,问:
中元素的个数,问:
![]() 若函数
若函数![]() ,若
,若![]() ,则
,则![]() 是否等于0?若是,请证明,
是否等于0?若是,请证明,
![]() 若
若![]() ,试问:
,试问:![]() 是否一定等于1?若是,请证明
是否一定等于1?若是,请证明
(1)证明:先证 任取![]() ,则
,则![]()
![]()
再证 任取![]()
若![]() ,不妨设
,不妨设![]()
由单调递增可知:![]() 与
与![]() 矛盾
矛盾
同理![]() 也矛盾,所以
也矛盾,所以![]()
![]()
综上:![]()
(2)①若![]() 由于
由于![]() 无实根 则对任意实数x,
无实根 则对任意实数x,![]()
从而![]() 故
故![]() 无实根
无实根
同理若![]() 对任意实数x,
对任意实数x, ![]() ,从而
,从而![]()
故![]() 也无实根
也无实根
![]()
②不妨设![]() 是B中唯一元素 则
是B中唯一元素 则![]()
令![]() 那么
那么![]() 而
而![]()
故![]()
![]() 说明t也是
说明t也是![]() 的不动点
的不动点
由于 ![]() 只有唯一的不动点 故
只有唯一的不动点 故![]() 即
即![]()
这说明t也是![]() 的不动点,从而存在性得证
的不动点,从而存在性得证
以下证明唯一性:若![]() 还有另外一个不动点m,即
还有另外一个不动点m,即![]()
则![]() 这说明
这说明![]()
![]() 还有另外一个稳定点m
还有另外一个稳定点m
与题设矛盾。

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数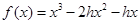 ,若
,若 且
且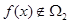 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得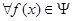 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


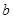
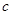




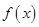 ,若
,若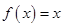 ,则称
,则称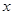 为
为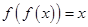 ,则称
,则称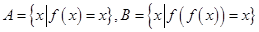
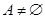 ,若
,若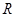 上单调递增函数,是否有
上单调递增函数,是否有 ?若是,请证明。
?若是,请证明。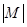 表示集合
表示集合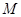 中元素的个数,问:
中元素的个数,问: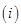 若函数
若函数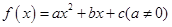 ,若
,若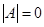 ,则
,则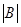 是否等于0?若是,请证明
是否等于0?若是,请证明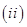 若
若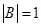 ,试问:
,试问: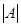 是否一定等于1?若是,请证明
是否一定等于1?若是,请证明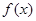 ,若存在
,若存在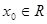 ,使
,使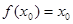 成立,则称
成立,则称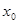 为
为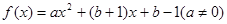 ,若对任意实数b,函数
,若对任意实数b,函数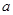 的取值范围是 ( )
的取值范围是 ( )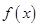 ,若存在
,若存在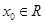 ,使得
,使得 成立,则称
成立,则称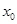 为
为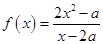 ,若
,若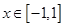 内存在“滞点”,求
内存在“滞点”,求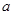 的取值范围.
的取值范围.