Question

如图，圆x²+y²=8内有一点P（-1，2），AB为过点P且倾斜角为α的弦，
（1）当α=135°时，求|AB|
（2）当弦AB被点P平分时，写出直线AB的方程．
（3）求过点P的弦的中点的轨迹方程．

Answer 1

分析：（1）过点O做OG⊥AB于G，连接OA，依题意可知直线AB的斜率，求得AB的方程，利用点到直线的距离求得OG即圆的半径，进而求得OA的长，则OB可求得．
（2）弦AB被P平分时，OP⊥AB，则OP的斜率可知，利用点斜式求得AB的方程．
（3）设出AB的中点的坐标，依据题意联立方程组，消去k求得x和y的关系式，即P的轨迹方程．

解答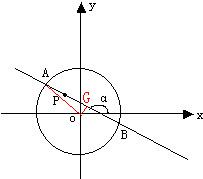：解：（1）过点O做OG⊥AB于G，连接OA，当α=135⁰时，直线AB的
斜率为-1，故直线AB的方程x+y-1=0，∴OG=

|0+0-1|

2

=

2

2

∵r=2

2

∴AG=

8- 1 2

=

15 2

=

30

2

，
∴|AB|=2AG=

30

（2）当弦AB被P平分时，OP⊥AB，此时K_OP=-2，
∴AB的点斜式方程为y-2=

1

2

（x+1），即x-2y+5=0
（3）设AB的中点为M（x，y），AB的斜率为K，OM⊥AB，则

y-2=k(x+1) y=- 1 k x

消去K，得x²+y²-2y+x=0，当AB的斜率K不存在时也成立，
故过点P的弦的中点的轨迹方程为x²+y²-2y+x=0

点评：本题主要考查了直线与圆的方程的综合运用．解题的过程通过代数的运算解决代数问题，最后翻译成几何结论．