题目内容
如图,经过圆x2+y2=4上任意一点P作x轴的垂线,垂足为Q,求线段PQ中点M的轨迹方程.

x2+4y2=4即为所求轨迹方程.
解析:
(代入法)设M(x,y),P(x0,y0),则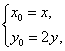 又P(x0,y0)在圆x2+y2=4上,
又P(x0,y0)在圆x2+y2=4上,
∴x02+y02=4.
∴x2+4y2=4即为所求轨迹方程.

练习册系列答案
相关题目
题目内容
如图,经过圆x2+y2=4上任意一点P作x轴的垂线,垂足为Q,求线段PQ中点M的轨迹方程.

x2+4y2=4即为所求轨迹方程.
(代入法)设M(x,y),P(x0,y0),则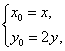 又P(x0,y0)在圆x2+y2=4上,
又P(x0,y0)在圆x2+y2=4上,
∴x02+y02=4.
∴x2+4y2=4即为所求轨迹方程.
