题目内容
有3个相识的人某天各自乘火车外出,假设火车有10节车厢,那么至少有2人在同一车厢内相遇的概率为( )
A. | B. | C. | D. |
B
解析试题分析:三人上10节车厢的情况种数是10×10×10=1000,
三人在不同的车厢的情况种数是: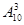 =10×9×8,
=10×9×8,
∴至少两人上了同一车厢的概率=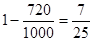 .
.
考点:古典概型及其概率计算公式.
点评:本题考查的是等可能事件的概率的求法,所求的事件的概率等于用1减去它的对立事件概率.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=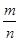 ,属于基础题.
,属于基础题.

练习册系列答案
相关题目
一个三位数字的密码键,每位上的数字都在0到9这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为( )
| A.1/1000 | B.1/100 | C.1/10 | D.1/9 |
设 为两个事件,且
为两个事件,且 ,
, ,则( )
,则( )
A. 与 与 互斥 互斥 | B. 与 与 对立 对立 | C. | D.A、B、C都不对 |
随机变量 服从二项分布
服从二项分布 ~
~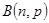 ,且
,且 则
则 等于( )
等于( )
A. | B.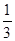 | C.1 | D.0 |
 B.
B. C.
C.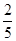 D.
D.




 中,
中, ,顶点
,顶点 处分别有一枚半径为1的硬币(顶点
处分别有一枚半径为1的硬币(顶点



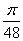
 则满足
则满足 的学生成绩情况的概率是
的学生成绩情况的概率是




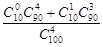

 .
.