题目内容
一个三位数字的密码键,每位上的数字都在0到9这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为( )
| A.1/1000 | B.1/100 | C.1/10 | D.1/9 |
C
解析试题分析:由已知中一个三位数字的密码锁,每位上的数字都在0到9这十个数字中任选,某人忘记了密码最后一个号码,我们易求出基本事件总数为10,满足条件的基本事件个数为1,代入古典概型概率计算公式,即可求出答案.解:由于最后一位上取值在0到9这十个数字中任选,则基本事件共有10种,其中随意拨动最后一个数字恰好能开锁的基本事件只有一种故随意拨动最后一个数字恰好能开锁的概率为0.1故选C
考点:古典概型
点评:本题考查的知识点是古典概型及其概率计算公式,其中根据已知条件求出基本事件总数及满足条件的基本事件个数,是解答本题的关键

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,若生产中出现乙级品的概率为0.03,丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
| A.0.99 | B.0.98 | C.0.97 | D.0.96 |
从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm的概率为 ( )
| A.0.8 | B.0.7 | C.0.3 | D.0.2 |
一个不透明的口袋中装有形状相同的红球、黄球和蓝球,若摸出一球为红球的概率为 ,黄球的概率为
,黄球的概率为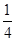 ,袋中红球有4个,则袋中蓝球的个数为( ).
,袋中红球有4个,则袋中蓝球的个数为( ).
| A.5个 | B.11个 | C.4个 | D.9个 |
 ,则事件A在一次试验中出现的概率是
,则事件A在一次试验中出现的概率是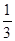




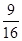


 服从的分布列如图,则随机变量
服从的分布列如图,则随机变量 等于 ( )
等于 ( )




 B.
B. C.
C.  D.
D. 
 (所以判断性别与运动有关,那么这种判断出错的可能性为( )(注:
(所以判断性别与运动有关,那么这种判断出错的可能性为( )(注: )
)






