题目内容
. (本小题满分12分)
已知函数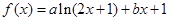 .
.
(1)若函数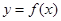 在
在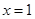 处取得极值,且曲线
处取得极值,且曲线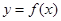 在点
在点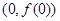 处的切线与直线
处的切线与直线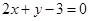 平行,求
平行,求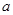 和
和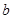 的值;
的值;
(2)若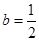 ,试讨论函数
,试讨论函数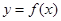 的单调性.
的单调性.
已知函数
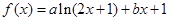 .
.(1)若函数
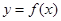 在
在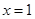 处取得极值,且曲线
处取得极值,且曲线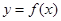 在点
在点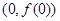 处的切线与直线
处的切线与直线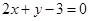 平行,求
平行,求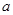 和
和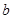 的值;
的值;(2)若
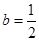 ,试讨论函数
,试讨论函数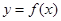 的单调性.
的单调性.(1)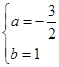 ;(2)当
;(2)当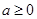 时,函数
时,函数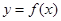 在
在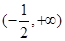 上是增函数;
上是增函数;
当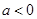 时,函数
时,函数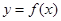 在
在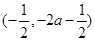 上为减函数,在
上为减函数,在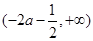 上是增函数.
上是增函数.
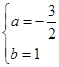 ;(2)当
;(2)当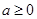 时,函数
时,函数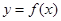 在
在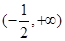 上是增函数;
上是增函数;当
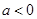 时,函数
时,函数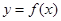 在
在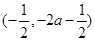 上为减函数,在
上为减函数,在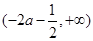 上是增函数.
上是增函数. 第一问考查函数的切线与直线平行。在求函数切线时,要注意“过某点的切线”与“在某点的切线”的区别。第二问考查利用函数的导数讨论含参数的函数的单调性问题。注意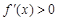 不是函数递增的充要条件。
不是函数递增的充要条件。
解:(1)∵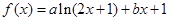
∴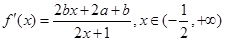 …………………………2分
…………………………2分
由题意的得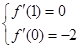 …………………………4分
…………………………4分
即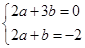 解得
解得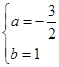 ………………………6分
………………………6分
(2)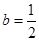 时,
时,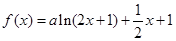
∴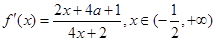 …………………………8分
…………………………8分
∵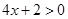
∴当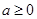 时,在定义域
时,在定义域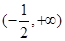 内
内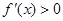 恒成立,函数单调递增,………10分
恒成立,函数单调递增,………10分
当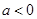 时,由
时,由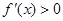 得
得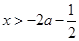 ,
,
由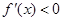 得
得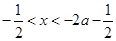 ,
,
综上:当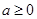 时,函数
时,函数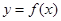 在
在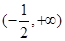 上是增函数;
上是增函数;
当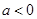 时,函数
时,函数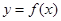 在
在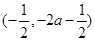 上为减函数,
上为减函数,
在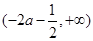 上是增函数. …………………………12分
上是增函数. …………………………12分
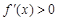 不是函数递增的充要条件。
不是函数递增的充要条件。解:(1)∵
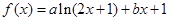
∴
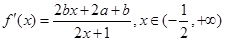 …………………………2分
…………………………2分由题意的得
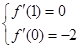 …………………………4分
…………………………4分即
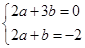 解得
解得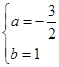 ………………………6分
………………………6分(2)
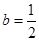 时,
时,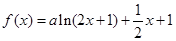
∴
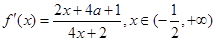 …………………………8分
…………………………8分∵
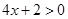
∴当
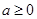 时,在定义域
时,在定义域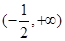 内
内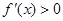 恒成立,函数单调递增,………10分
恒成立,函数单调递增,………10分当
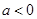 时,由
时,由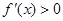 得
得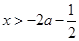 ,
,由
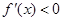 得
得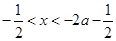 ,
,综上:当
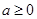 时,函数
时,函数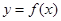 在
在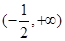 上是增函数;
上是增函数;当
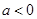 时,函数
时,函数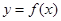 在
在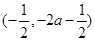 上为减函数,
上为减函数,在
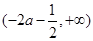 上是增函数. …………………………12分
上是增函数. …………………………12分
练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
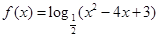 的单调递增区间是
的单调递增区间是 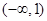
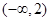
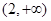
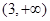
 (x2-2x-3)的单调递增区间是__________.
(x2-2x-3)的单调递增区间是__________.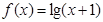 ,
,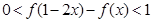 ,求
,求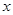 的取值范围;
的取值范围;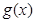 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当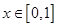 时,
时,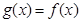 ,当
,当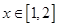 时,求函数
时,求函数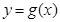 的取值范围.
的取值范围.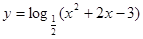 的单调递减区间是_____________.
的单调递减区间是_____________.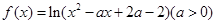 ,若
,若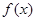 在
在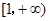 上是增函数,则
上是增函数,则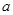 的取值范围是 .
的取值范围是 .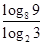 的值为( )
的值为( )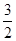
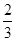
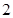
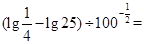 .
.