Question

已知矩形ABCD，AB＝1，BC＝，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，下列说法正确的是________．(填序号)

①存在某个位置，使得直线AC与直线BD垂直；

②存在某个位置，使得直线AB与直线CD垂直；

③存在某个位置，使得直线AD与直线BC垂直；

④对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直．

 

Answer 1

②

【解析】找出图形在翻折过程中变化的量与不变的量．

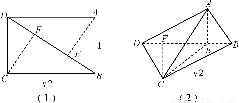
对于①，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F，在图(1)中，由边AB、BC不相等可知点E、F不重合．在图(2)中，连结CE，若直线AC与直线BD垂直，∵AC∩AE＝A，∴BD⊥平面ACE，∴BD⊥CE，与点E、F不重合相矛盾，故①错误．

对于②，若AB⊥CD，∵AB⊥AD，AD∩CD＝D，∴AB⊥平面ADC，∴AB⊥AC，由AB<BC可知存在这样的等腰直角三角形，使得直线AB与直线CD垂直，故②正确．

对于③，若AD⊥BC，∵DC⊥BC，AD∩DC＝D，∴BC⊥平面ADC，∴BC⊥AC.已知BC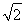＝，AB＝1，BC>AB，∴不存在这样的直角三角形．∴③错误．

由上可知④错误，故正确的说法只有②.