题目内容
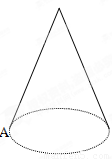
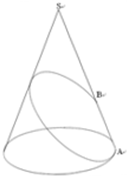 如图,圆锥的母线长为4cm,底面直径为2cm.
如图,圆锥的母线长为4cm,底面直径为2cm.
(1)求圆锥的体积;(2)若在母线SA上取一点B,使得AB=1cm,求由点A绕圆锥一周回到点B的最短距离.
解:(1)设圆锥的高为h,底面半径为r,r=1,母线SA=4.
∴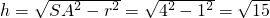
圆锥的体积为:V= ×π×
×π× =
= .
.
(2)设圆锥的侧面展开图为SAA',
则由点A绕圆锥一周回到点B的最短距离为BA'
∵ ,
,
SB=3,SA'=4∴BA'=5(cm)
由点A绕圆锥一周回到点B的最短距离5cm.
分析:(1)设圆锥的高为h,底面半径为r,r=1,母线SA=4.利用直角三角形即可求得高,从而得出其体积大小;
(2)设圆锥的侧面展开图为SAA',则由点A绕圆锥一周回到点B的最短距离为BA'求出侧面展开图中两点间的距离即为最短距离.
点评:考查圆锥的体积、圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.
∴
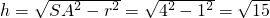
圆锥的体积为:V=
 ×π×
×π× =
= .
.(2)设圆锥的侧面展开图为SAA',
则由点A绕圆锥一周回到点B的最短距离为BA'
∵
 ,
,SB=3,SA'=4∴BA'=5(cm)
由点A绕圆锥一周回到点B的最短距离5cm.
分析:(1)设圆锥的高为h,底面半径为r,r=1,母线SA=4.利用直角三角形即可求得高,从而得出其体积大小;
(2)设圆锥的侧面展开图为SAA',则由点A绕圆锥一周回到点B的最短距离为BA'求出侧面展开图中两点间的距离即为最短距离.
点评:考查圆锥的体积、圆锥侧面展开图中两点间距离的求法;把立体几何转化为平面几何来求是解决本题的突破点.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
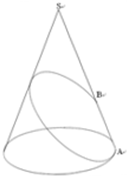 如图,圆锥的母线长为4cm,底面直径为2cm.
如图,圆锥的母线长为4cm,底面直径为2cm. 已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为
已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为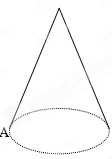 已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为________.
已知如图所示圆锥的母线长为6,底面半径为1,现有一只蚂蚁从底面圆的A点出发,绕圆锥侧面一圈后回到点A,则这只蚂蚁爬过的最短距离为________.