题目内容
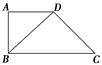
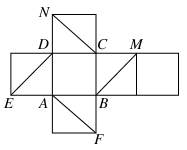
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
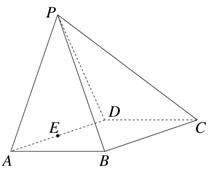
(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.

(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
(1)见解析 (2)

(1)连接PE、EB、BD,因为平面PAD⊥平面ABCD,△PAD为等边三角形,E为AD的中点,所以PE⊥AD,PE⊥平面ABCD,因为四边形ABCD为菱形,且∠DAB=60°,所以△ABD为等边三角形.
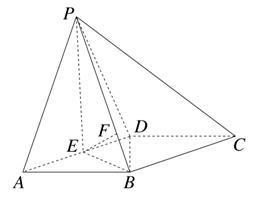
又E为AD的中点,所以BE⊥AE.
又PE∩BE=E,所以AD⊥平面PBE,所以AD⊥PB.
(2)过E作EF⊥PB交PB于点F,由(1)知AD⊥平面PBE,
因为AD∥BC,所以BC⊥平面PBE,
所以平面BPC⊥平面PBE,又平面PBC∩平面PBE=PB,故EF⊥平面PBC.
故点E到平面PBC的距离EF=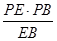 =
= .
.

又E为AD的中点,所以BE⊥AE.
又PE∩BE=E,所以AD⊥平面PBE,所以AD⊥PB.
(2)过E作EF⊥PB交PB于点F,由(1)知AD⊥平面PBE,
因为AD∥BC,所以BC⊥平面PBE,
所以平面BPC⊥平面PBE,又平面PBC∩平面PBE=PB,故EF⊥平面PBC.
故点E到平面PBC的距离EF=
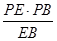 =
= .
.
练习册系列答案
相关题目
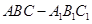 中,
中,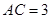 ,
,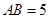 ,
,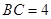 ,
,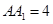 ,点
,点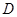 是
是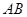 的中点.
的中点.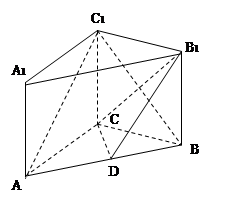
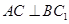 ;
; 
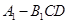 的体积.
的体积.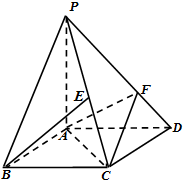
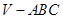 中,
中,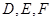 分别是
分别是 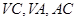 的中点,
的中点,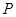 为
为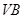 上任意一点,则直线
上任意一点,则直线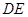 与
与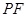 所成的角的大小是 ( )
所成的角的大小是 ( )
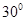
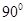
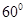

 ;②一定存在平行于a的平面
;②一定存在平行于a的平面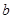 ∥
∥ ;④一定存在无数个平行于a的平面
;④一定存在无数个平行于a的平面