题目内容
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为| 2 | 3 |
分析:根据题意,分析可得甲比赛的局数可能为3、4、5,即X可取的值为3,4,5;分别求出X=3、4、5时的概率,注意求解时分甲、乙获胜两种情况,进而由期望的公式,计算可得答案.
解答:解:根据题意题意,分析可得X可取的值为3,4,5;
当X=3时,分甲、乙胜两种情况;
即甲连胜三局,其概率为(
)3=
,乙连胜三局,其概率为(
)3=
,
则P(X=3)=
=
;
当X=4时,也分甲、乙胜两种情况;
若甲胜,其概率为[C32(
)2×
]×
=
,若乙胜,其概率为[C32(
)2×
]×
=
,
则P(X=4)=
=
;
当X=5时,也分甲、乙胜两种情况;
若甲胜,其概率为[C42(
)2×(
)2]×
=
,若乙胜,其概率为[C32(
)2×(
)2]×
=
,
则P(X=5)=
;
则X的数学期望EX=3×
+4×
+5×
=
;
故答案为:
.
当X=3时,分甲、乙胜两种情况;
即甲连胜三局,其概率为(
| 2 |
| 3 |
| 8 |
| 27 |
| 1 |
| 3 |
| 1 |
| 27 |
则P(X=3)=
| 8+1 |
| 27 |
| 1 |
| 3 |
当X=4时,也分甲、乙胜两种情况;
若甲胜,其概率为[C32(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 27 |
则P(X=4)=
| 8+2 |
| 27 |
| 10 |
| 27 |
当X=5时,也分甲、乙胜两种情况;
若甲胜,其概率为[C42(
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
则P(X=5)=
| 8 |
| 27 |
则X的数学期望EX=3×
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
故答案为:
| 107 |
| 27 |
点评:本题考查期望的计算,计算期望,首先涉及概率的计算,解本题时,注意要分甲、乙获胜两种情况分析.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
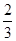 。
。