题目内容
已知定义域为R的二次函数f(x)的最小值为0且有f(1+x)=f(1-x),直线g(x)=4(x-1)被f(x)的图象截得的弦长为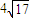 ,数列{an}满足,(an+1-an)g(an)+f(an)=0(n∈N*).
,数列{an}满足,(an+1-an)g(an)+f(an)=0(n∈N*).(1)函数f(x);
(2)求数列{an}的通项公式;
(3)设bn=3f(an)-g(an+1),求数列{bn}的最值及相应的n.
【答案】分析:(I)设f(x)=a(x-1)2(a>0),则直线g(x)=4(x-1)与y=f(x)图象的两个交点为(1,0), ,由
,由 ,由此得到f(x).
,由此得到f(x).
(II)由(an+1-an)•4(an-1)+(an-1)2=0,知(an-1)(4an+1-3an-1)=0∵a1=2,所以an≠1,4an+1-3an-1=0,由此能求出数列{an}的通项公式.
(III)bn=3(an-1)2-4(an+1-1)= .令
.令 则
则 .数列{bn}的最值及相应的n.
.数列{bn}的最值及相应的n.
解答:解:(I)设f(x)=a(x-1)2(a>0),则直线g(x)=4(x-1)与y=f(x)图象的两个交点为(1,0), ∵
∵ ∴a=1,f(x)=(x-1)2…(3分)
∴a=1,f(x)=(x-1)2…(3分)
(II)∵(an+1-an)•4(an-1)+(an-1)2=0∴
(an-1)(4an+1-3an-1)=0∵a1=2,∴an≠1,4an+1-3an-1=0
∴ 数列{an-1}是首项为1,公比为
数列{an-1}是首项为1,公比为 的等比数列
的等比数列
∴ …(9分)
…(9分)
(III)bn=3(an-1)2-4(an+1-1)=
令 则
则 ∵n∈N*,
∵n∈N*,
∴u的值分别为 …,经比较
…,经比较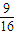 距
距 最近,
最近,
∴当n=3时,bn有最小值是 ,当n=1时,bn有最大值是0.…(14分)
,当n=1时,bn有最大值是0.…(14分)
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
 ,由
,由 ,由此得到f(x).
,由此得到f(x).(II)由(an+1-an)•4(an-1)+(an-1)2=0,知(an-1)(4an+1-3an-1)=0∵a1=2,所以an≠1,4an+1-3an-1=0,由此能求出数列{an}的通项公式.
(III)bn=3(an-1)2-4(an+1-1)=
 .令
.令 则
则 .数列{bn}的最值及相应的n.
.数列{bn}的最值及相应的n.解答:解:(I)设f(x)=a(x-1)2(a>0),则直线g(x)=4(x-1)与y=f(x)图象的两个交点为(1,0),
 ∵
∵ ∴a=1,f(x)=(x-1)2…(3分)
∴a=1,f(x)=(x-1)2…(3分)(II)∵(an+1-an)•4(an-1)+(an-1)2=0∴
(an-1)(4an+1-3an-1)=0∵a1=2,∴an≠1,4an+1-3an-1=0
∴
 数列{an-1}是首项为1,公比为
数列{an-1}是首项为1,公比为 的等比数列
的等比数列∴
 …(9分)
…(9分)(III)bn=3(an-1)2-4(an+1-1)=

令
 则
则 ∵n∈N*,
∵n∈N*,∴u的值分别为
 …,经比较
…,经比较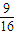 距
距 最近,
最近,∴当n=3时,bn有最小值是
 ,当n=1时,bn有最大值是0.…(14分)
,当n=1时,bn有最大值是0.…(14分)点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目