题目内容
已知函数f(x)=1+lnx.
(1) 求过原点且与曲线y=f(x)相切的直线方程;
(2) 若关于x的不等式f(x)≤ax恒成立,求实数a的取值范围.
解:(1)∵f(x)=1+lnx,∴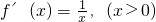 ,
,
设曲线y=f(x)上切点坐标为(x0,1+lnx0),
则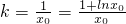 ,解得x0=1,k=1,
,解得x0=1,k=1,
∴切线方程为y=x.(5分)
(2)∵x>0,
∴f(x)≤ax?a≥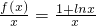 ,(6分)
,(6分)
设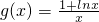 ,则
,则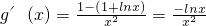 ,(8分)
,(8分)
令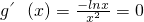 ,得x=1,(9分)
,得x=1,(9分)
当0<x<1时,g'(x)>0,g(x)在(0,1)上为增函数,
当x>1时,g'(x)<0,g(x)在(1,+∞)上为减函数,
∴g(x)max=g(1)=1,
∴a≥1.(12分)
分析:(1) 先求其导函数,设出切点坐标,进而得切线的斜率,求出切线方程,利用切线过原点,就可以把具体的切线方程求出来;
(2)先把不等式f(x)≤ax恒成立转化为a≥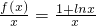 ,再利用导函数求出不等式右边的最大值即可求出实数a的取值范围.
,再利用导函数求出不等式右边的最大值即可求出实数a的取值范围.
点评:本题主要考查利用导数研究曲线上某点切线方程以及研究函数在某个闭区间上的最值问题,是对知识的综合考查,属于中档题.
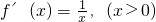 ,
,设曲线y=f(x)上切点坐标为(x0,1+lnx0),
则
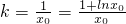 ,解得x0=1,k=1,
,解得x0=1,k=1,∴切线方程为y=x.(5分)
(2)∵x>0,
∴f(x)≤ax?a≥
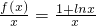 ,(6分)
,(6分)设
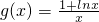 ,则
,则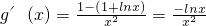 ,(8分)
,(8分)令
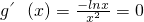 ,得x=1,(9分)
,得x=1,(9分)当0<x<1时,g'(x)>0,g(x)在(0,1)上为增函数,
当x>1时,g'(x)<0,g(x)在(1,+∞)上为减函数,
∴g(x)max=g(1)=1,
∴a≥1.(12分)
分析:(1) 先求其导函数,设出切点坐标,进而得切线的斜率,求出切线方程,利用切线过原点,就可以把具体的切线方程求出来;
(2)先把不等式f(x)≤ax恒成立转化为a≥
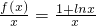 ,再利用导函数求出不等式右边的最大值即可求出实数a的取值范围.
,再利用导函数求出不等式右边的最大值即可求出实数a的取值范围.点评:本题主要考查利用导数研究曲线上某点切线方程以及研究函数在某个闭区间上的最值问题,是对知识的综合考查,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|