题目内容
设x,y满足约束条件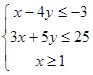 ,求目标函数z=6x+10y的最大值是
,求目标函数z=6x+10y的最大值是
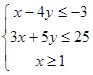 ,求目标函数z=6x+10y的最大值是
,求目标函数z=6x+10y的最大值是 50
试题分析: 根据题意作出不等式组表示的平面区域,得到三角形的可行域,当目标函数平移到由直线x-4y+3=0,3x+5y=25,的交点(1,
 )时目标函数取得最大值,且为6+10
)时目标函数取得最大值,且为6+10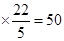 ,故答案为50.
,故答案为50.点评:解决该试题的关键是准确的作图,虚实要分,然后利用目标函数的斜率与区域内直线的斜率的关系来得到最优解。

练习册系列答案
相关题目
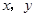 满足
满足 则
则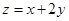 的最小值是 ( )
的最小值是 ( ) 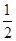
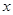 、
、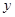 满足约束条件
满足约束条件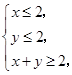 ,
,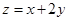 的最大值;(2)求目标函数
的最大值;(2)求目标函数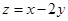 的最小值.
的最小值.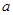 、
、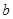 ,则集合
,则集合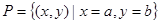 所表示的平面图形面积等于
所表示的平面图形面积等于 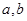 满足约束条件
满足约束条件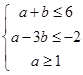 ,
,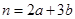 ,则
,则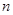 取最小值时,
取最小值时, 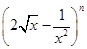 二项展开式中的常数项为 ( )
二项展开式中的常数项为 ( ) 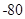
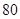
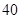
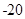
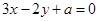 两侧,则
两侧,则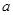 的范围是
的范围是
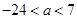
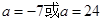
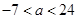
 满足不等式组
满足不等式组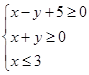 ,那么目标函数
,那么目标函数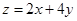 的最小值是 ( )
的最小值是 ( )