题目内容
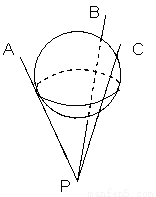
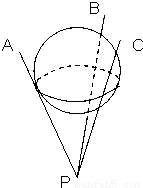
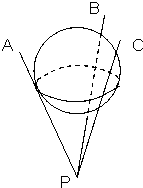如图所示，是一个由三根细铁杆PA，PB，PC组成的支架，三根铁杆的两两夹角都是60°，一个半径为1的球放在支架上，则球心到P的距离为| 3 |
| 3 |
分析：利用三根铁杆的两两夹角都是60°，可得△ABC和△PAB为正三角形，再利用三角形相似，可得比例式，由此即可求得OP的值．
解答：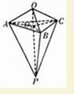
解：连接OP交平面ABC于O'，
∵三根铁杆的两两夹角都是60°，
∴△ABC和△PAB为正三角形，
∴O′A=
AB=
PA
∵AO′⊥PO，OA⊥PA，
∴△AO′P∽△OAP
∴
=
∴OP=
OA
∵半径OA=1
∴OP=
故答案为：
解：连接OP交平面ABC于O'，∵三根铁杆的两两夹角都是60°，
∴△ABC和△PAB为正三角形，
∴O′A=
| ||
| 3 |
| ||
| 3 |
∵AO′⊥PO，OA⊥PA，
∴△AO′P∽△OAP
∴
| AO′ |
| AP |
| OA |
| OP |
∴OP=
| 3 |
∵半径OA=1
∴OP=
| 3 |
故答案为：
| 3 |
点评：本题考查棱锥知识，考查三角形的相似，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
,
,
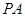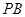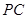组成的支架，三根铁杆的两两夹角都是
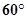，一个半径为1的球放在支架上，则球心到
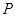的距离为____________
,
,
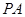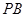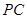组成的支架，三根铁杆的两两夹角都是
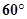，一个半径为1的球放在支架上，则球心到
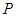的距离为 _ 
