题目内容
设定义在区间[-1,1]上的偶函数f(x)与函数g(x)的图象关于直线x=1对称,且当x∈[2,3]时,g(x)=| a | 3 |
分析:根据函数是一个偶函数,f(x) 在区间[-1,1]上的最大值与最小值,实际上分别等于f(x) 在区间[-1,0]上最大值与最小值,f(x)与函数g(x)的图象关于直线x=1对称,f(x) 在区间[-1,0]上最大值与最小值,也就是g(x)在区间[2,3]上的最大值与最小值,利用导数求g(x)在区间[2,3]上的最大值与最小值,得到结果.
解答:解:∵f(x)为定义在区间[-1,1]上的偶函数,
∴f(x) 在区间[-1,1]上的最大值与最小值,
实际上分别等于f(x) 在区间[-1,0]上最大值与最小值.
∵f(x)与函数g(x)的图象关于直线x=1对称,
∴f(x) 在区间[-1,0]上最大值与最小值,也就是g(x)在区间[2,3]上的最大值与最小值.(4分)
g′(x)=
-12(x-2)2.
∵0<a<36,
∴g′(x)=0的二根为2±
,其中2<2+
<3,2-
<2.
∴列表如下:
∴(f(x))max=(g(x))max=g(2+
)=
.(f(x))min=(g(x))min=min(g(2),g(3))=
(13分)
∴f(x) 在区间[-1,1]上的最大值与最小值,
实际上分别等于f(x) 在区间[-1,0]上最大值与最小值.
∵f(x)与函数g(x)的图象关于直线x=1对称,
∴f(x) 在区间[-1,0]上最大值与最小值,也就是g(x)在区间[2,3]上的最大值与最小值.(4分)
g′(x)=
| a |
| 3 |
∵0<a<36,
∴g′(x)=0的二根为2±
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |
∴列表如下:
| x | [2,2+
|
2+
|
(2+
| ||||||||||||
| g′(x) | >0 | =0 | <0 | ||||||||||||
| g(x) | ↗ |
|
↘ |
| ||
| 6 |
a
| ||
| 27 |
|
点评:本题考查导数在求最值中的应用和函数的奇偶性及对称性,本题解题的关键是通过分析函数的性质,看出题目的实质,再利用导数求最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
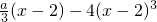 (0<a<36),求f(x)的最大值与最小值.
(0<a<36),求f(x)的最大值与最小值.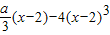 (0<a<36),求f(x)的最大值与最小值.
(0<a<36),求f(x)的最大值与最小值.