题目内容
下列不等式中,解集是R的是( )
分析:对于A,利用不等式求出tanx的范围,判断是否满足题意.
对于B,通过二倍角公式,求出x的解集,即可判断正误;
对于C,根据三角函数的定义域,求出x的范围,即可判断正误;
对于D,根据定义域,直接判断是否满足题意.
对于B,通过二倍角公式,求出x的解集,即可判断正误;
对于C,根据三角函数的定义域,求出x的范围,即可判断正误;
对于D,根据定义域,直接判断是否满足题意.
解答:解:因为tan2x+tanx+1>0,△<0,所以x∉R;A不正确;
因为sin2x+
cos2x+
+sin2x>0,所以sin2x+
cos2x+
+
-
cos2x>0,
即sin2x+1>0,x∉R,所以B不正确;
因为cos(sinx)>0,显然x∈R,满足题意;
因为lg(2+sinx)>0,所以2+sinx>1,x∉R,所以D不正确;
故选C.
因为sin2x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即sin2x+1>0,x∉R,所以B不正确;
因为cos(sinx)>0,显然x∈R,满足题意;
因为lg(2+sinx)>0,所以2+sinx>1,x∉R,所以D不正确;
故选C.
点评:本题是基础题,考查三角函数的定义域,二倍角公式的应用,考查不等式的基本性质,考查计算能力,逻辑推理能力.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
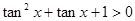 B.
B.
 D.
D.
