题目内容
正四面体ABCD中,AO⊥平面BCD,垂足为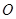 ,设
,设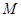 是线段
是线段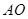 上一点,且
上一点,且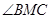 是直角,则
是直角,则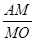 的值为 .
的值为 .
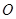 ,设
,设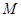 是线段
是线段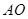 上一点,且
上一点,且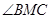 是直角,则
是直角,则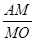 的值为 .
的值为 .1.
试题分析:延长BO,交CD于点N,可得BN⊥CD且N为CD中点
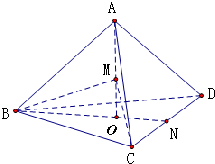
设正四面体ABCD棱长为1,得等边△ABC中,BN=
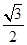 ,BC=
,BC=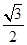
∵AO⊥平面BCD,∴O为等边△ABC的中心,得BO=
 ,BN=
,BN=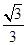 ,
,Rt△ABO中,AO=
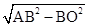 =
=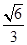
设MO=x,则Rt△BOM中,BM=
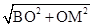 =
=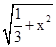
∵∠BMC=90°,得△BMC是等腰直角三角形,
∴BM=AM=
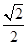 BC,即
BC,即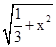 =
=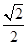 ,解之得x=
,解之得x=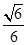
由此可得AM=AO-MO=
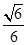 ,所以MO=AM=
,所以MO=AM=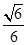 ,从而
,从而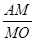 =1.
=1.点评:中档题,本题充分借助于正四面体的几何性质,通过发现等腰三角形,灵活利用勾股定理,达到解题目的。本题解法充分体现了立体几何问题转化成平面几何问题的基本思路。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 中,
中, ,
, ,
, 是底面对角线的交点.
是底面对角线的交点.
 平面
平面 ;
; 平面
平面 的体积。
的体积。
 与直线
与直线 均垂直于
均垂直于 所在平面,且
所在平面,且 ,
,
 平面
平面 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.


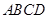 中,
中, 为正三角形,
为正三角形,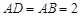 ,
, ,
, 与
与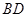 交于
交于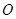 点.将
点.将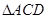 沿边
沿边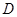 点至
点至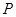 点,已知
点,已知 与平面
与平面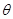 ,且
,且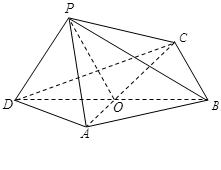
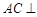 平面
平面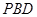 ;
;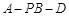 的余弦值为
的余弦值为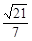 ,求
,求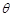 的大小.
的大小.