题目内容
当兔子和狐狸处于同一栖息地时,忽略其他因素,只考虑兔子数量和狐狸数量的相互影响,为了简便起见,不妨做如下假设:(1)由于自然繁殖,兔子数每年增长10%,狐狸数每年减少15%;
(2)由于狐狸吃兔子,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍;
(3)第n年时,兔子数量Rn用表示,狐狸数量用Fn表示;
(4)初始时刻(即第0年),兔子数量有R=100只,狐狸数量有F=30只.
请用所学知识解决如下问题:
(1)列出兔子与狐狸的生态模型;
(2)求出Rn、Fn关于n的关系式;
(3)讨论当n越来越大时,兔子与狐狸的数量是否能达到一个稳定的平衡状态,说明你的理由.
【答案】分析:(1)根据兔子数每年增长10%,狐狸数每年减少15%,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍,可得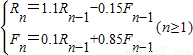
(2)利用矩阵,求出矩阵的特征多项式,从而可求矩阵的特征值、特征向量,由此可求Rn、Fn关于n的关系式;
(3)当n越来越大时,0.95n越来越接近于0,Rn,Fn分别趋向于常量210,140.由此可知,时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态.
解答:解:(1)∵兔子数每年增长10%,狐狸数每年减少15%,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍
∴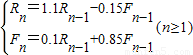 …4’
…4’
(2)设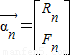 ,
,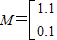
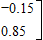
∴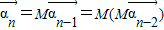 =…=
=…=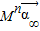
又矩阵M的特征多项式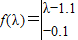
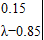 =λ2-1.95λ+0.95=(λ-1)(λ-0.95)
=λ2-1.95λ+0.95=(λ-1)(λ-0.95)
令f(λ)=0得:λ1=1,λ2=0.95
特征值λ1=1对应的一个特征向量为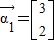
特征值λ2=0.95对应的一个特征向量为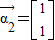 …6’
…6’
且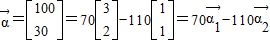
∴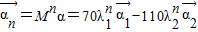 =
=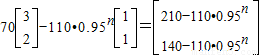
∴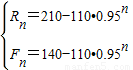 …14’
…14’
(3)当n越来越大时,0.95n越来越接近于0,Rn,Fn分别趋向于常量210,140.即随着时间的增加,兔子与狐狸的数量逐渐增加,当时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态.…2’
点评:本题以实际问题为载体,考查矩阵的运用,考查特征值与特征向量,考查利用数学知识解决实际问题.
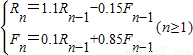
(2)利用矩阵,求出矩阵的特征多项式,从而可求矩阵的特征值、特征向量,由此可求Rn、Fn关于n的关系式;
(3)当n越来越大时,0.95n越来越接近于0,Rn,Fn分别趋向于常量210,140.由此可知,时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态.
解答:解:(1)∵兔子数每年增长10%,狐狸数每年减少15%,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍
∴
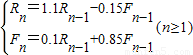 …4’
…4’(2)设
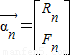 ,
,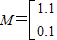
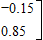
∴
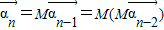 =…=
=…=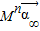
又矩阵M的特征多项式
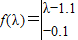
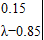 =λ2-1.95λ+0.95=(λ-1)(λ-0.95)
=λ2-1.95λ+0.95=(λ-1)(λ-0.95)令f(λ)=0得:λ1=1,λ2=0.95
特征值λ1=1对应的一个特征向量为
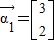
特征值λ2=0.95对应的一个特征向量为
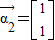 …6’
…6’且
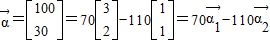
∴
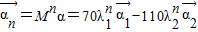 =
=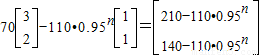
∴
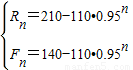 …14’
…14’(3)当n越来越大时,0.95n越来越接近于0,Rn,Fn分别趋向于常量210,140.即随着时间的增加,兔子与狐狸的数量逐渐增加,当时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态.…2’
点评:本题以实际问题为载体,考查矩阵的运用,考查特征值与特征向量,考查利用数学知识解决实际问题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目