(1)求(1+x+x2+x3)(1-x)7的展开式中x4的系数,(2)求(x+4x-4)4的展开式中的常数项,3+(1+x)4+-+(1+x)50的展开式中x3的系数．题目和参考答案——青夏教育精英家教网—

题目内容

（1）求（1+x+x²+x³）（1-x）⁷的展开式中x⁴的系数；
（2）求（x+

-4）⁴的展开式中的常数项；
（3）求（1+x）³+（1+x）⁴+…+（1+x）⁵⁰的展开式中x³的系数．

分析：（1）由等比数列的前n项和公式，可将原式化为（1-x⁴）（1-x）⁶，进而分析x⁴取得的情况，计算可得答案，
（2）对（x+

-4）⁴变形可得

(2-x)8

，分析可得，要在展开式中取得常数项，则必须在（2-x）⁸中取得x⁴项，进而由二项式定理，计算可得答案；
（3）根据题意，原式可变形为

(1+x)51-(1+x)3

，要在展开式中取得x³项，必须在（1+x）⁵¹取得x⁴项，进而由二项式定理，计算可得答案．

解答：解：（1）原式=

1-x4

1-x

（1-x）⁷=（1-x⁴）（1-x）⁶，
展开式中x⁴的有两种情况，在（1-x⁴）中取（-x⁴），在（1-x）⁶中取1，或在（1-x⁴）中取（1），在（1-x）⁶中取x²，
其系数为（-1）⁴C₆⁴-1=14．
（2）（x+

-4）⁴=

(x2-4x+4)4

(2-x)8

，
要在展开式中取得常数项，则必须在（2-x）⁸中取得x⁴项，
故其原式的展开式中常数项为C₈⁴2⁴•（-1）4=1120．
（3）原式=

(1+x)3[(1+x)48-1]

(1+x)-1

(1+x)51-(1+x)3

；
要在展开式中取得x³项，必须在（1+x）⁵¹取得x⁴项，
故其原式的展开式中x³的系数为C₅₁⁴．

点评：把所给式子转化为二项展开式形式是解决此类问题的关键．

练习册系列答案

相关题目

，5]，其中m是不等于零的常数，
（1）（理）写出h（4x）的定义域；
（文）m=1时，直接写出h（x）的值域；
（2）（文、理）求h（x）的单调递增区间；
（3）已知函数f（x）（x∈[a，b]），定义：f₁（x）=minf（t）|a≤t≤x（x∈[a，b]），f₂（x）=maxf（t）|a≤t≤x（x∈[a，b]）．其中，minf（x）|x∈D表示函数f（x）在D上的最小值，maxf（x）|x∈D表示函数f（x）在D上的最大值．例如：f（x）=cosx，x∈[0，π]，则f₁（x）=cosx，x∈[0，π]，f₂（x）=1，x∈[0，π]．
（理）当m=1时，设M(x)=

h(x)+h(4x)

|h(x)-h(4x)|

，不等式t≤M₁（x）-M₂（x）≤n恒成立，求t，n的取值范围；
（文）当m=1时，|h₁（x）-h₂（x）|≤n恒成立，求n的取值范围．

仔细阅读下面问题的解法：
设A=[0，1]，若不等式2^1-x+a＞0在A上有解，求实数a的取值范围．
解：令f（x）=2^1-x+a，因为f（x）＞0在A上有解．

⇒f(x)在A上的最大值大于0，

又∵f(x)在[0，1]上单调递减

⇒f(x)最大值=f(0)
=2+a＞0⇒a＞-2
学习以上问题的解法，解决下面的问题，已知：函数f（x）=x²+2x+3（-2≤x≤-1）．
①求f（x）的反函数f^-1（x）及反函数的定义域A；
②设B={x|lg

10-x

10+x

＞lg(2x+a-5)}，若A∩B≠∅，求实数a的取值范围．

已知函数f（x）=mx+n的图象经过点A（1，2），B（-1，0），且函数h(x)=2p

（p＞0）与函数f（x）=mx+n的图象只有一个交点．
（1）求函数f（x）与h（x）的解析式；
（2）设函数F（x）=f（x）-h（x），求F（x）的最小值与单调区间；
（3）设a∈R，解关于x的方程log₄[f（x-1）-1]=log₂h（a-x）-log₂h（4-x）．

设g（x）=2x+

，x∈[

，4]．
（1）求g（x）的单调区间；（简单说明理由，不必严格证明）
（2）证明g（x）的最小值为g（

）；
（3）设已知函数f（x）（x∈[a，b]），定义：f₁（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f₂（x）=max{f（t）|a≤t≤x}（x∈[a，b]．其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值．例如：f（x）=sinx，x∈[-

，不等式p≤φ₁（x）-φ₂（x）≤m恒成立，求p、m的取值范围．

已知：函数

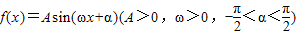的最小正周期是π，且当

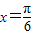时f（x）取得最大值3．
（1）求f（x）的解析式及单调增区间．
（2）若x∈[0，2π），且

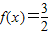，求x．
（3）将函数f（x）的图象向右平移m（m＞0）个单位长度后得到函数y=g（x）的图象，且y=g（x）是偶函数，求m的最小值．

试题分类