题目内容
若函数y=a2x+b+1(a>0且a≠1,b为实数)的图象恒过定点(1,2),求b的值 .
【答案】分析:令解析式中的指数2x+b=0求出x的值,再代入解析式求出y的值,即得到定点的坐标,结合条件列出关于b的方程,解之即得.
解答:解:令2x+b=0解得,x=-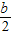 ,代入y=a2x+b+1得,y=2,
,代入y=a2x+b+1得,y=2,
∴函数图象过定点(-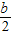 ,2),
,2),
又函数y=a2x+b+1(a>0且a≠1,b为实数)的图象恒过定点(1,2),
∴-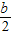 =1,
=1,
∴b=-2
故答案为:-2.
点评:本题考查了指数函数的单调性与特殊点、指数函数的图象过定点(0,1)的应用,即令解析式中的指数为0求出对应的x和y的值.
解答:解:令2x+b=0解得,x=-
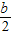 ,代入y=a2x+b+1得,y=2,
,代入y=a2x+b+1得,y=2,∴函数图象过定点(-
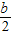 ,2),
,2),又函数y=a2x+b+1(a>0且a≠1,b为实数)的图象恒过定点(1,2),
∴-
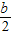 =1,
=1,∴b=-2
故答案为:-2.
点评:本题考查了指数函数的单调性与特殊点、指数函数的图象过定点(0,1)的应用,即令解析式中的指数为0求出对应的x和y的值.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目