��Ŀ����
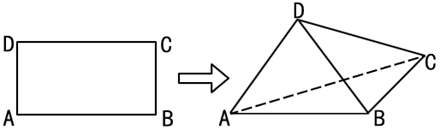
����Ŀ�����й�ʣ�ඨ�����ֳ������Ӷ�������1852�꣬Ӣ����������ʿΰ���������������㾭�������ﲻ֪��������Ľⷨ����ŷ�ޣ�1874�꣬Ӣ����ѧ������ɭָ���˷�����1801���ɸ�˹�õ��Ĺ���ͬ��ʽ�ⷨ��һ���Զ��������������֮Ϊ���й�ʣ�ඨ���������й�ʣ�ඨ����������һ���������������⣬��������һ���������⣺��1��2019��2019�����У��ܱ�3����2�ұ�5������2��������С�����˳���ų�һ�У���������![]() ����������������У��м����ֵΪ��������
����������������У��м����ֵΪ��������
A.992B.1022C.1007D.1037
���𰸡�C
��������
���Ƚ���Ŀת��Ϊ![]() ����3�ı�����Ҳ��5�ı�����Ҳ����15�ı���.��д��
����3�ı�����Ҳ��5�ı�����Ҳ����15�ı���.��д��![]() ��ͨ�ʽ�������м����.
��ͨ�ʽ�������м����.
����Ŀת��Ϊ![]() ����3�ı�����Ҳ��5�ı�����Ҳ����15�ı���.
����3�ı�����Ҳ��5�ı�����Ҳ����15�ı���.
��![]() ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ������
������![]() �����
�����![]() �
�
��������м���Ϊ��![]() �
�![]() .
.
�ʴ�Ϊ��C��

����Ŀ��2014�꣬�������Ժ�칫��ӡ������������ũ�����ؾ�ӪȨ������ת��չũҵ�ʶȹ�ģ��Ӫ���������Ҫ�������չ������ת���ʶȹ�ģ��Ӫ.ij������2015�꿪ʼ�а���һ�����Ĵ��ģˮ����ֲˮ����������һ��ˮ���ո������̨������ˮ���ո������ʹ���������ӣ�ÿ���������Ҳ��Ӧ���ӣ�����ˮ���ո���Թ���ʹ��֮����5������ƽ��ÿ̨ˮ���ո����������������ͳ�����£�
��� | 2015 | 2016 | 2017 | 2018 | 2019 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 |
�������� | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
��1������5���������ȡ2�꣬��ƽ��ÿ̨ˮ���ո��ÿ�����������������1�����2��Ԫ�ĸ��ʣ�
��2����![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��3������ˮ���ո���Ĺ���۸���ÿ̨16��Ԫ����(2)�еĻع鷽�̣���ÿ̨ˮ���ո������ƽ�����ýǶȣ�����Ϊһ̨��ˮ���ո����ʹ����5�����̭�����Ǽ���ʹ�õ���8������̭��
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��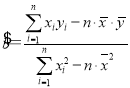 ��
��![]()
![]() .
.