题目内容
下列函数,奇函数是
- A.f(x)=lnx
- B.f(x)=ex
- C.f(x)=sinx+x
- D.f(x)=cosx+x2
C
分析:先求函数的定义域,判断其是否关于原点对称,然后探讨f(-x)与f(x)的关系,即可得 函数的奇偶性.
解答:选项A,定义域为(0,+∞),不关于原点对称,故f(x)=lnx不是奇函数.
选项B,定义域为R,e-x≠ex,故f(x)=ex不是奇函数.
选项C,定义域为R,(-x)+sin(-x)=-(x+sinx),故f(x)=x+sinx为奇函数.
选项D,定义域为R,cos(-x)+(-x)2=cosx+x2,故f(x)=xcosx为偶函数,
故选C.
点评:本题考查了函数的奇偶性的判断---定义法,注意定义域,是个基础题.
分析:先求函数的定义域,判断其是否关于原点对称,然后探讨f(-x)与f(x)的关系,即可得 函数的奇偶性.
解答:选项A,定义域为(0,+∞),不关于原点对称,故f(x)=lnx不是奇函数.
选项B,定义域为R,e-x≠ex,故f(x)=ex不是奇函数.
选项C,定义域为R,(-x)+sin(-x)=-(x+sinx),故f(x)=x+sinx为奇函数.
选项D,定义域为R,cos(-x)+(-x)2=cosx+x2,故f(x)=xcosx为偶函数,
故选C.
点评:本题考查了函数的奇偶性的判断---定义法,注意定义域,是个基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
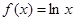 B.
B. C.
C. D.
D.
