题目内容
函数f(x)=ln(4+3x-x2)的单调递减区间是
A.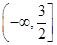 B.
B.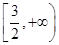 C.
C.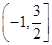 D.
D.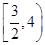
【答案】
D
【解析】
试题分析:令u=4+3x-x2,因为y=lnu是增函数,所以u=4+3x-x2应满足,是增函数,且u>0;解4+3x-x2>0,得,-1<x<4,所以函数f(x)=ln(4+3x-x2)的单调递减区间是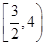 ,选D。
,选D。
考点:本题主要考查复合对数函数的单调性。
点评:简单题,复合函数的单调性,遵循“内外层函数,‘同增异减’”。涉及对数函数,特别注意定义域。

练习册系列答案
相关题目
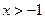 ,证明:
,证明: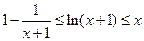 .
. x2+x-m(m为常数)的图象上P点处的切线与直线x-
x2+x-m(m为常数)的图象上P点处的切线与直线x- y+2=0的夹角为45°,则点P的横坐标为(
)
y+2=0的夹角为45°,则点P的横坐标为(
) C.
C.  D. ±
D. ±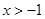 ,证明:
,证明: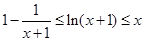 .
.