题目内容
学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为
的样本，其频率分布直方图如右图所示，其中支出在
元的同学有39人，则的值为
| A．100 | B．120 | C．130 | D．390 |
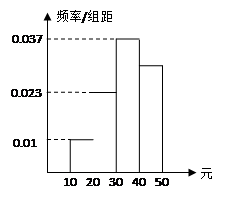
C
解析考点：用样本的频率分布估计总体分布．
专题：计算题．
分析：根据频率直方图的意义，由前三个小组的频率可得样本在[40，50）元的频率，计算可得样本容量．
解答：解：由题意可知：前三个小组的频率之和=（0.01+0.023+0.037）×10=0.7，
∴支出在[40，50）元的频率为1-0.7=0.3，
∴n的值=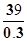
=130；
故选C．
点评：本题是对频率、频数灵活运用的综合考查，各小组频数之和等于数据总和，各小组频率之和等于1．频率、频数的关系：频率= 
．
练习册系列答案
精英口算卡系列答案
相关题目
对两个变量y和x进行回归分析，得到一组样本数据（x1,y1）,（x2,y2）,…,（xn,yn），则下列说法中不正确的是
A．由样本数据得到的回归方程  =bx+a必过点 |
| B．残差平方和越小的模型，拟合的效果越好 |
C．用相关指数 来刻画回归效果, 越小，说明模型的拟合效果越好 |
| D．若变量y和x之间的相关系数为r=-0.9362，则变量y和x之间具有线性相关关系 |
某校数学教研组为了解学生学习数学的情况，采用分层抽样的方法从高一600人、高二680人、高三720人中，抽取50人进行问卷调查，则高一、高二、高三抽取的人数分别是
| A．15,16,19 | B．15,17,18 | C．14,17,19 | D．15,16,20 |
已知回归方程
则
A． =1.5 －15 | B． 15是回归系数a |
| C． 1.5是回归系数a | D．x =10时，y=0 |
某工厂生产某种产品的产量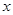
（吨）与相应的生产能耗
（吨标准煤）有如下几组样本数据：
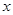| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
A、
B、
C、
D、
某商场有四类商品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测，若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是 （ ）
| A．4 | B．5 | C．6 | D．7 |
某牛奶生产线上每隔30分钟抽取一袋进行检验，则该抽样方法为①；从某中学的30名数学爱好者中抽取3人了解学习负担情况，则该抽样方法为②.那么（ ）
| A．①是系统抽样，②是简单随机抽样 | B．①是分层抽样，②是简单随机抽样 | C．①是系统抽样，②是分层抽样 | D．①是分层抽样，②是系统抽样 |