题目内容
已知向量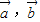 满足
满足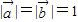 ,且
,且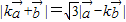 ,(k>0)令
,(k>0)令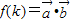
(1)求
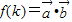 (用k表示);
(用k表示);(2)当k>0时,
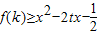 对任意的t∈[-1,1]恒成立,求实数x的取值范围.
对任意的t∈[-1,1]恒成立,求实数x的取值范围.
【答案】分析:(1)直接利用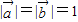 ,结合
,结合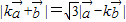 两边平方整理即可得到结论;
两边平方整理即可得到结论;
(2)当 k>0时,先根据基本不等式求出f(k)的最小值,再把所求问题转化为g(t)=-2xt+x2-1<0对任意的t∈[-1,1]恒成立,最后结合一次函数的知识即可得到实数x的取值范围.
解答:解:(1)由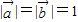 ,
,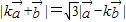
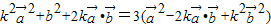
整理得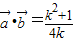
∴f(k)=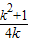 (k>0)…(4分)
(k>0)…(4分)
(2)当 k>0时f(k)=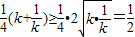
(当且当k=1时等号成立)…(6分)
∴当 k>0时f(k)≥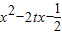 对任意的t∈[-1,1]恒成立
对任意的t∈[-1,1]恒成立
即 ≥
≥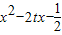
亦即x2-2tx-1≤1对任意的t∈[-1,1]恒成立…(8分)
而x2-2tx-1=-2xt+x2-1=g(t)
∴g(t)=-2xt+x2-1<0对任意的t∈[-1,1]恒成立
由一次函数的性质可得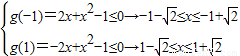 …(10分)
…(10分)
∴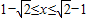
∴实数的取值范围为[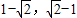 ]
]
点评:本题主要考查平面向量的基本运算性质,数量积的运算性质,等价转化思想,以及恒成立问题和基本不等式的运用.是对知识的综合考查,属于中档题目.
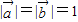 ,结合
,结合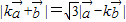 两边平方整理即可得到结论;
两边平方整理即可得到结论;(2)当 k>0时,先根据基本不等式求出f(k)的最小值,再把所求问题转化为g(t)=-2xt+x2-1<0对任意的t∈[-1,1]恒成立,最后结合一次函数的知识即可得到实数x的取值范围.
解答:解:(1)由
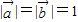 ,
,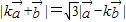
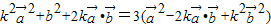
整理得
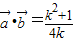
∴f(k)=
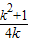 (k>0)…(4分)
(k>0)…(4分)(2)当 k>0时f(k)=
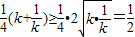
(当且当k=1时等号成立)…(6分)
∴当 k>0时f(k)≥
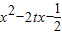 对任意的t∈[-1,1]恒成立
对任意的t∈[-1,1]恒成立即
 ≥
≥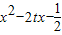
亦即x2-2tx-1≤1对任意的t∈[-1,1]恒成立…(8分)
而x2-2tx-1=-2xt+x2-1=g(t)
∴g(t)=-2xt+x2-1<0对任意的t∈[-1,1]恒成立
由一次函数的性质可得
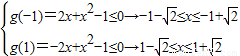 …(10分)
…(10分)∴
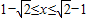
∴实数的取值范围为[
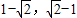 ]
]点评:本题主要考查平面向量的基本运算性质,数量积的运算性质,等价转化思想,以及恒成立问题和基本不等式的运用.是对知识的综合考查,属于中档题目.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
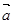 ,
,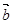 满足
满足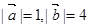 ,且
,且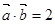 ,则
,则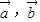 满足
满足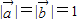 ,且
,且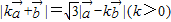 ,令
,令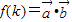 ,
,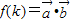 (用k表示);
(用k表示);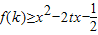 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.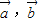 满足
满足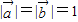 ,且
,且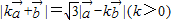 ,令
,令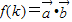 ,
,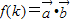 (用k表示);
(用k表示);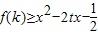 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.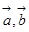 满足
满足 ,且
,且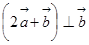 .
.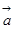 的坐标; (2)、求向量
的坐标; (2)、求向量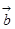 的夹角.
的夹角.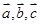 满足
满足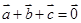 ,且
,且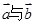 的夹角为135°,
的夹角为135°,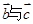 的夹角为120°,
的夹角为120°,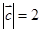 ,则
,则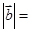 _____________;
_____________;