题目内容
已知向量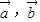 满足
满足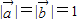 ,且
,且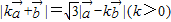 ,令
,令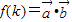 ,
,(1)求
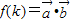 (用k表示);
(用k表示);(2)当k>0时,
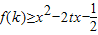 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.
【答案】分析:(Ⅰ)利用条件把已知的等式两边平方展开整理易得函数f(k)的解析式.
(Ⅱ)由基本不等式求的函数f(k)的最小值等于 ,问题等价于
,问题等价于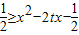 在[-1,1]上恒成立,故即g(t)=2xt-x2+1≥0在[-1,1]上恒成立,而g(t)在[-1,1]上为单调函数或常函数,所以
在[-1,1]上恒成立,故即g(t)=2xt-x2+1≥0在[-1,1]上恒成立,而g(t)在[-1,1]上为单调函数或常函数,所以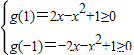 ,由此求得实数x的取值范围.
,由此求得实数x的取值范围.
解答:解:(Ⅰ)由题设得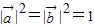 ,对
,对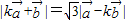 ,
,
两边平方得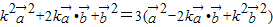 . …(2分)
. …(2分)
展开整理易得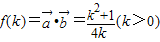 .…(4分)
.…(4分)
(Ⅱ)∵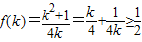 ,当且仅当k=1时取得等号.…(6分)
,当且仅当k=1时取得等号.…(6分)
欲使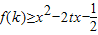 对任意的t∈[-1,1]恒成立,等价于
对任意的t∈[-1,1]恒成立,等价于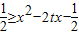 …(7分)
…(7分)
即g(t)=2xt-x2+1≥0在[-1,1]上恒成立.
而g(t)在[-1,1]上为单调函数或常函数,
所以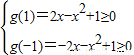 ,…(11分)
,…(11分)
解得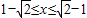 ,…(13分)
,…(13分)
故实数x的取值范围为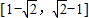 . …(14分)
. …(14分)
点评:本题主要考查两个向量的数量积的运算,以及函数的恒成立问题,求出函数f(k)的解析式,是解题的突破口,属于中档题.
(Ⅱ)由基本不等式求的函数f(k)的最小值等于
 ,问题等价于
,问题等价于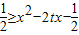 在[-1,1]上恒成立,故即g(t)=2xt-x2+1≥0在[-1,1]上恒成立,而g(t)在[-1,1]上为单调函数或常函数,所以
在[-1,1]上恒成立,故即g(t)=2xt-x2+1≥0在[-1,1]上恒成立,而g(t)在[-1,1]上为单调函数或常函数,所以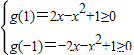 ,由此求得实数x的取值范围.
,由此求得实数x的取值范围.解答:解:(Ⅰ)由题设得
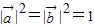 ,对
,对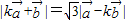 ,
,两边平方得
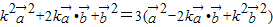 . …(2分)
. …(2分)展开整理易得
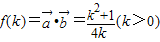 .…(4分)
.…(4分)(Ⅱ)∵
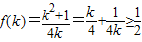 ,当且仅当k=1时取得等号.…(6分)
,当且仅当k=1时取得等号.…(6分)欲使
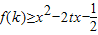 对任意的t∈[-1,1]恒成立,等价于
对任意的t∈[-1,1]恒成立,等价于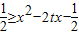 …(7分)
…(7分)即g(t)=2xt-x2+1≥0在[-1,1]上恒成立.
而g(t)在[-1,1]上为单调函数或常函数,
所以
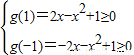 ,…(11分)
,…(11分) 解得
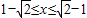 ,…(13分)
,…(13分)故实数x的取值范围为
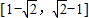 . …(14分)
. …(14分)点评:本题主要考查两个向量的数量积的运算,以及函数的恒成立问题,求出函数f(k)的解析式,是解题的突破口,属于中档题.

练习册系列答案
相关题目
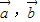 满足
满足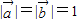 ,且
,且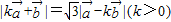 ,令
,令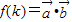 ,
,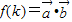 (用k表示);
(用k表示);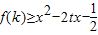 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.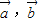 满足
满足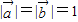 ,且
,且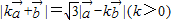 ,令
,令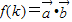 ,
,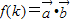 (用k表示);
(用k表示);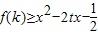 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围. 满足
满足 ,且
,且 ,令
,令 ,
, (用k表示);
(用k表示); 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.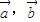 满足
满足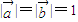 ,且
,且 ,令
,令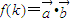 ,
,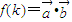 (用k表示);
(用k表示);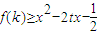 对任意的t∈[-1,1]恒成立,求实数x取值范围.
对任意的t∈[-1,1]恒成立,求实数x取值范围.