题目内容
1.在正项等比数列{an}中,若a1•a9=4,则log2a1+log2a2+log2a3+…+log2a9=9.分析 直接利用等比数列的性质以及对数的运算法则化简所求表达式,求解即可.
解答 解:∵a1•a9=4,∴a1•a9=a2•a8=a3•a7=a4•a6=4
∴log2a1+log2a2+log2a3+…+log2a9=log2(a1•a2•a3…a9)=log2(a1•${a}_{9})^{\frac{9}{2}}$=log229=9
故答案为:9.
点评 本题考查数列求和对数 的运算法则等比数列的性质,考查计算能力.

练习册系列答案
相关题目
11.如图,若N=2015时,则输出的数等于( )
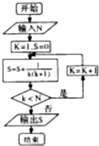

| A. | $\frac{2015}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2016}$ |
12.已知函数$f(x)=\frac{{sinx+cosx+|{sinx-cosx}|}}{2}$,则下列结论正确的是( )
| A. | f(x)是奇函数 | B. | f(x)在$[{0,\frac{π}{2}}]$上递增 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,1] |
16.在复平面内,复数$z=\frac{i}{2+i}$对应的点所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.函数y=sin($\frac{1}{2}$x+$\frac{π}{3}$)的周期为( )
| A. | 2π | B. | 4π | C. | π | D. | 3π |
 如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$).
如图,在平面直角坐标系xOy中,角α以x轴非负半轴为始边,其终边与单位圆交于点P,过点P作x轴的垂线与射线y=$\sqrt{3}$x(x≥0)交于点Q,其中α∈(-$\frac{π}{2}$,$\frac{π}{2}$). .
. 时,求函数
时,求函数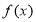 的定义域;
的定义域;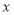 的不等式
的不等式 的解集是
的解集是 ,求
,求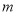 的取值范围.
的取值范围. ,则
,则 ( )
( ) B.
B.
 D
D