题目内容

已知集合M={f（x）|f2（x）-f2（y）=f（x+y）•f（x-y）}，x，y∈R，有下列命题：
①若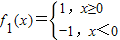则f1（x）∈M；
②若f2（x）=sinx，则f2（x）∈M；
③若f（x）∈M，y=f（x）的图象关于原点对称；
④若f（x）∈M，则对任意不等的实数x1、x2，总有；
⑤若f（x）∈M，则对任意的实数x1、x2，总有．
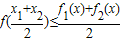其中是正确的命题有    ．（写出所有正确命题的编号）
【答案】分析：通过举反例，判断出①错；通过三角函数的和差公式判断出②对；通过给x，y赋值及奇函数的定义判断出③对；通过举反例，判断出④错；通过举反例判断出⑤错．
解答：解：对于①令x≥y≥0，f2（x）-f2（y）=0而f（x+y）f（x-y）=1，则易知①是错误的；
对于②f2（x）-f2（y）=sin2x-sin2y，f（x+y）f（x-y）=sin2x-sin2y有②f2（x）-f2（y）=f（x+y）f（x-y）
故②是正确的；
对于③令x=y=0可得f（0）=0；再令x=0，有f2（0）-f2（y）=f（y）f（-y）即f（y）（（fy）+f（-y））=0则有f（y）=0或f（-y）=-f（y），因此f（x）为奇函数，故③正确；
令f（x）=sinx∈M但f（x）在R上不具备单调性，故④错，同样借助f（x）=sinx的图象，验证⑤不正确
故答案为：②③
点评：本题考查三角函数的和、差角公式、考查奇函数的定义、考查利用举反例的方法说明一个命题不成立．
练习册系列答案
相关题目
8、已知集合M={f（x）|f（-x）=f（x），x∈R}；N={f（x）|f（-x）=-f（x），x∈R}；P={f（x）|f（1-x）=f（1+x），x∈R}；Q={f（x）|f（1-x）=-f（1+x），x∈R}；若f（x）=（x-1）3，x∈R，则下列关系中正确的序列号为：
④

①f（x）∈M②f（x）∈N③f（x）∈P④f（x）∈Q
已知集合M={f（x）|f2（x）-f2（y）=f（x+y）•f（x-y）}，x，y∈R，有下列命题：
①若f1(x)=
1，x≥0
-1，x＜0
则f1（x）∈M；
②若f2（x）=sinx，则f2（x）∈M；
③若f（x）∈M，y=f（x）的图象关于原点对称；
④若f（x）∈M，则对任意不等的实数x1、x2，总有
f1(x)-f2(x)
x1-x2
＜0；
⑤若f（x）∈M，则对任意的实数x1、x2，总有f(
x1+x2
2
)≤
f1(x)+f2(x)
2
．
其中是正确的命题有
 
．（写出所有正确命题的编号）
（2013•南充三模）已知集合M={f（x）|f2（x）-f2（y）=f（x+y）•f（x-y），x，y∈R}，有下列命题
①若f1（x）=
1，x≥0
-1，x＜0
则f1（x）∈M；
②若f2（x）=2x，则f2（x）∈M；
③若f3（x）∈M，则y=f3（x）的图象关于原点对称；
④若f4（x）∈M则对于任意不等的实数x1，x2，总有
f4(x1)-f4(x2)
x1-x2
＜0成立．
其中所有正确命题的序号是
②③
②③
．
已知集合M={f（x）|在定义域内存在实数x0，使得f（x0+1）=f（x0）+f（1）成立}．
（1）函数f（x）=
1
x
是否属于集合M？说明理由．
（2）证明：函数f（x）=2x+x2∈M．
（3）设函数f（x）=lg
a
2x+1
∈M，求实数a的取值范围．
（2007•上海模拟）已知集合M={f（x）|f（x）+f（x+2）=f（x+1），x∈R}，g(x)=sin
πx3
．
（1）判断g（x）与M的关系，并说明理由；
（2）M中的元素是否都是周期函数，证明你的结论；
（3）M中的元素是否都是奇函数，证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网