题目内容
设 是等差数列
是等差数列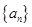 的前
的前 项和,已知
项和,已知 ,
,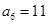 ,则
,则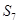 等于
等于
| A.13 | B.35 | C.49 | D.63 |
C
解析试题分析:因为根据等差中项的性质可知,a1+a7=a2+a6=3+11=14,那么则
故答案为49,选C.
考点:本题主要考查学生掌握等差数列的性质及前n项和的公式,是一道基础题.
点评:解决该试题的关键是根据等差数列的性质可知项数之和相等的两项之和相等即a1+a7=a2+a6,求出a1+a7的值,然后利用等差数列的前n项和的公式表示出S7,将a1+a7的值代入即可求出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
“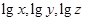 成等差数列”是“
成等差数列”是“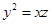 ”成立的( )
”成立的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
等差数列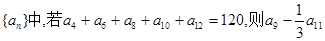 的值是( )
的值是( )
| A.14 | B.15 | C.16 | D.17 |
在数列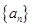 中,
中, ,
,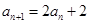 ,则
,则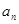 等于( )
等于( )
A.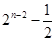 | B.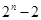 | C.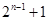 | D.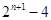 |
已知等差数列{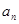 }的前2006项的和
}的前2006项的和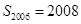 ,其中所有的偶数项的和是2,则
,其中所有的偶数项的和是2,则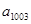 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
已知递增等差数列 中,
中,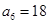 且
且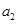 是
是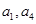 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为
| A.180 | B.198 | C.189 | D.168 |
已知等差数列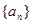 中,
中,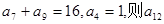 的值是 ( )
的值是 ( )
A.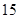 | B.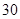 | C. 31 | D. 64 |
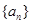 的前
的前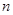 项和为
项和为 ,关于数列
,关于数列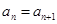 ;
;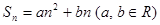 ,则数列
,则数列 ,则数列
,则数列