题目内容
如图,已知 平面
平面 ,
, 平面
平面 ,△
,△ 为等边三角形,
为等边三角形, ,
, 为
为 的中点.
的中点.
(1) 求证: 平面
平面 ;
;
(2) 求证:平面 平面
平面 ;
;
(3) 求直线 和平面
和平面 所成角的正弦值.
所成角的正弦值.

【答案】
(1) 证:取 的中点
的中点 ,连
,连 .
.
∵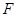 为
为 的中点,∴
的中点,∴ 且
且 . …………1分
. …………1分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ ,∴
,∴ .
…………2分
.
…………2分
又 ,∴
,∴ .
…………3分
.
…………3分
∴四边形 为平行四边形,则
为平行四边形,则 . …………4分
. …………4分
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
…………5分
.
…………5分
(2) 证:∵ 为等边三角形,
为等边三角形,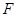 为
为 的中点,∴
的中点,∴ . ……6分
. ……6分
∵ 平面
平面 ,
, 平面
平面 ,∴
,∴ .
………7分
.
………7分
又 ,故
,故 平面
平面 .
…………8分
.
…………8分
∵ ,∴
,∴ 平面
平面 .
…………9分
.
…………9分
∵ 平面
平面 ,
,
∴平面 平面
平面 .
…………10分(3)
.
…………10分(3)
解:在平面 内,过
内,过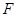 作
作 于
于 ,连
,连 .
.
∵平面 平面
平面 , ∴
, ∴ 平面
平面 .
.
∴ 为
为 和平面
和平面 所成的角.
…………12分
所成的角.
…………12分
设 ,则
,则 ,
,
 ,
,
R t△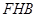 中,
中,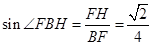 .
.
∴直线 和平面
和平面 所成角的正弦值为
所成角的正弦值为 .
.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8
(2013•滨州一模)如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8 平面
平面 ,
, 平面
平面 ,
, 为等边三角形,
为等边三角形, ,
, 为
为 中点.
中点.
 平面
平面 ;
; 平面
平面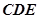 ;
; 与平面
与平面 如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8
如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠DAB=90°,AB∥CD,AD=AF=4,AB=2CD=8 (1)求证:
(1)求证: