题目内容
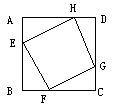
已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点, 且AE=BF=CG=DH, 设小正方形EFGH的面积为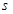 ,AE为
,AE为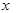 ,则
,则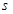 关于
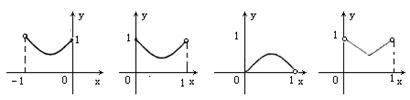
关于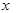 的函数图象大致是( )
的函数图象大致是( )
A B C D
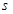 ,AE为
,AE为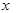 ,则
,则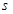 关于
关于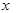 的函数图象大致是( )
的函数图象大致是( )

A B C D
B
∵根据正方形的四边相等,四个角都是直角,且AE=BF=CG=DH,
∴可证△AEH≌△BFE≌△CGF≌△DHG.
设AE为x,则AH=1-x,根据勾股定理,得
EH2=AE2+AH2=x2+(1-x)2
即s=x2+(1-x)2.
s=2x2-2x+1,
∴所求函数是一个开口向上,对称轴是直线x= .∴自变量的取值范围是大于0小于1.故选B.
.∴自变量的取值范围是大于0小于1.故选B.
∴可证△AEH≌△BFE≌△CGF≌△DHG.
设AE为x,则AH=1-x,根据勾股定理,得
EH2=AE2+AH2=x2+(1-x)2
即s=x2+(1-x)2.
s=2x2-2x+1,
∴所求函数是一个开口向上,对称轴是直线x=
 .∴自变量的取值范围是大于0小于1.故选B.
.∴自变量的取值范围是大于0小于1.故选B.
练习册系列答案
相关题目
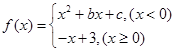 ,若
,若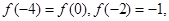

 的解析式;
的解析式; 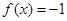 ,求相应
,求相应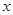 的值.
的值.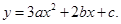
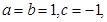 求该抛物线与
求该抛物线与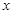 轴公共点的坐标;
轴公共点的坐标;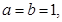 且当
且当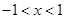 时,抛物线与
时,抛物线与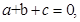 且
且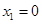 时,
时,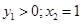 时,
时,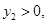 试判断当
试判断当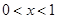 时,抛物线与
时,抛物线与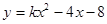 在区间
在区间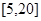 上是减函数,则实数k的取值范围为 .
上是减函数,则实数k的取值范围为 . ,若
,若 在区间
在区间 上的最大值为1,则
上的最大值为1,则 的取
的取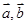 的夹角为120°,当
的夹角为120°,当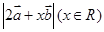 取得最小值时
取得最小值时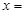 .
. 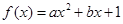 为定义在
为定义在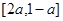 上的偶函数,则
上的偶函数,则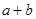 的值是( )
的值是( )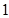
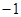
 或
或 或
或 满足
满足 ,则
,则 .
.