题目内容
某远洋捕渔船到远海捕鱼,由于远海渔业资源丰富,每撒一次网都有w万元的收益;同时,又由于远海风云未测,每撒一次网存在遭遇沉船事故的可能,其概率为
(常数k为大于1的正整数).假定,捕鱼船吨位很大,可以装下n次撒网所捕的鱼,而在每次撒网时,发生不发生沉船事故与前一次撒网无关,若发生沉船事故,则原来所获的收益将随船的沉没而不存在,又已知船长计划在此处撒网n次.(1)当n=3时,求捕鱼收益的期望值;
(2)试求n的值,使这次远洋捕鱼收益的期望值达到最大.
解:(1)列表:
收益 | 0 | 3ω |
P | 1-(1 | (1 |
)3所以收益的期望值=3w(1
)3.
(2)列表:
收益 | 0 | nω |
P | 1-(1 | (1 |
)n
)n因此,撒了n次网收益的期望值等于f(n)=wn(1
)n.
f(n+1)=w(n+1)(1
)n+1=wn(1
)n(1
)
=f(n)［1+
］.
∵［1+
］≥1等价于(k-1)-n≥0,得n≤k-1,
∴当n＜k-1时,f(n+1)＞f(n);当n=k-1时,f(n+1)=f(n);当n＞k-1时,f(n+1)＜f(n);
因此,当n=k-1时,f(n)达到最大.
练习册系列答案
相关题目
（常数k为大于l的正整数）。假定，捕鱼船吨位很大，可以装下几次撒网所捕的鱼，而在每次撒网时，发生不发生沉船事故与前一次撒网无关，若发生沉船事故，则原来所获的收益将随船的沉没而不存在，又已知船长计划在此处撒网n次。
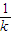（常数k为大于l的正整数）．假定，捕鱼船吨位很大，可以装下几次撒网所捕的鱼，而在每次撒网时，发生不发生沉船事故与前一次撒网无关，若发生沉船事故，则原来所获的收益将随船的沉没而不存在，又已知船长计划在此处撒网n次．