题目内容
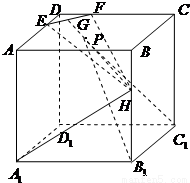
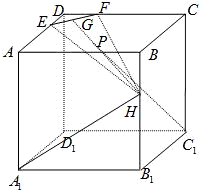 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
(1)求A1H与平面EFH所成角的余弦值;
(2)设点P在线段GH上,且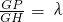 ,试确定λ的值,使得C1P的长度最短.
,试确定λ的值,使得C1P的长度最短.
解:由题意,以D1为坐标原点,A1D1,D1C1,DD1为x,y,z轴建立直角坐标系,
可得E(2,0,6),F(0,2,6),H(6,6,4),A1(6,0,0).
(1)设平面EFH的法向量 =(1,x,y),∵
=(1,x,y),∵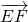 =(-2,2,0),
=(-2,2,0), =(4,6,-2)
=(4,6,-2)
∴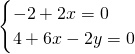 ,求得
,求得 =(1,1,5);
=(1,1,5);
∵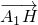 =(0,6,4),∴cos<
=(0,6,4),∴cos< ,
,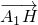 >=
>=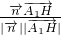 =
= =
= ;
;
设A1H 与平面EF所成角θ,则cosθ= =
= .(5分)
.(5分)
(2)由题意知,G(1,1,6),C1(0,6,0), =(5,5,-2),
=(5,5,-2),
∵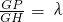 ,∴设
,∴设 =λ
=λ =(5λ,5λ,-2λ),解得P(5λ+1,5λ+1,-2λ+6),
=(5λ,5λ,-2λ),解得P(5λ+1,5λ+1,-2λ+6),
∴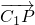 =(5λ+1,5λ-5,-2λ+6),
=(5λ+1,5λ-5,-2λ+6),
∴ =(5λ+1)2+(5λ-5)2+(2λ-6)2=54λ2-64λ+58,
=(5λ+1)2+(5λ-5)2+(2λ-6)2=54λ2-64λ+58,
当λ=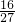 时,C1P的长度取得最小值.(10分)
时,C1P的长度取得最小值.(10分)
分析:(1)由题意建立坐标系,求出平面EFH的法向量,利用对应向量的数量积求出线面角的余弦值,再求其正弦值;
(2)由题意先求出P点的坐标,再求向量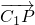 的长度的平方,转化为关于λ的一个一元二次函数,当取在对称轴出有最小值.
的长度的平方,转化为关于λ的一个一元二次函数,当取在对称轴出有最小值.
点评:本题用向量法求线面角的问题及求线段的最小值,只要用了向量的数量积和向量的长度;在求长度时转化到了二次函数求最小值,考查了转化思想和运算能力.
可得E(2,0,6),F(0,2,6),H(6,6,4),A1(6,0,0).
(1)设平面EFH的法向量
 =(1,x,y),∵
=(1,x,y),∵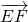 =(-2,2,0),
=(-2,2,0), =(4,6,-2)
=(4,6,-2)∴
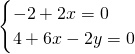 ,求得
,求得 =(1,1,5);
=(1,1,5);∵
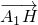 =(0,6,4),∴cos<
=(0,6,4),∴cos< ,
,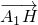 >=
>=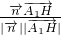 =
= =
= ;
;设A1H 与平面EF所成角θ,则cosθ=
 =
= .(5分)
.(5分)(2)由题意知,G(1,1,6),C1(0,6,0),
 =(5,5,-2),
=(5,5,-2),∵
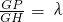 ,∴设
,∴设 =λ
=λ =(5λ,5λ,-2λ),解得P(5λ+1,5λ+1,-2λ+6),
=(5λ,5λ,-2λ),解得P(5λ+1,5λ+1,-2λ+6),∴
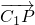 =(5λ+1,5λ-5,-2λ+6),
=(5λ+1,5λ-5,-2λ+6),∴
 =(5λ+1)2+(5λ-5)2+(2λ-6)2=54λ2-64λ+58,
=(5λ+1)2+(5λ-5)2+(2λ-6)2=54λ2-64λ+58,当λ=
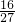 时,C1P的长度取得最小值.(10分)
时,C1P的长度取得最小值.(10分)分析:(1)由题意建立坐标系,求出平面EFH的法向量,利用对应向量的数量积求出线面角的余弦值,再求其正弦值;
(2)由题意先求出P点的坐标,再求向量
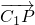 的长度的平方,转化为关于λ的一个一元二次函数,当取在对称轴出有最小值.
的长度的平方,转化为关于λ的一个一元二次函数,当取在对称轴出有最小值.点评:本题用向量法求线面角的问题及求线段的最小值,只要用了向量的数量积和向量的长度;在求长度时转化到了二次函数求最小值,考查了转化思想和运算能力.

练习册系列答案
相关题目
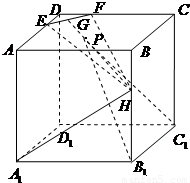
 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.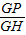 =λ,试确定λ的值,使得二面角P-C1B1-A1的余弦值为
=λ,试确定λ的值,使得二面角P-C1B1-A1的余弦值为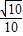 .
.
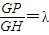 ,试确定λ的值,使得C1P的长度最短.
,试确定λ的值,使得C1P的长度最短.