题目内容
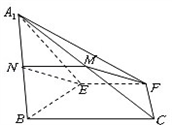
如图①,E,F分别是直角三角形ABC边AB和AC的中点,∠B=90°,沿EF将三角形ABC折成如图②所示的锐二面角A1﹣EF﹣B,若M为线段A1C中点.求证:
(1)直线FM∥平面A1EB;
(2)平面A1FC⊥平面A1BC.
(1)直线FM∥平面A1EB;
(2)平面A1FC⊥平面A1BC.

证明:(1)取A1B中点N,连接NE,NM,
则MN
 ,EF
,EF
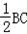 ,所以MN
,所以MN FE,
FE,
所以四边形MNEF为平行四边形,所以FM∥EN,
又因为FM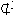 平面A1EB,EN
平面A1EB,EN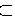 平面A1EB,
平面A1EB,
所以直线FM∥平面A1EB.
(2)因为E,F分别AB和AC的中点,
所以A1F=FC,所以FM⊥A1C
同理,EN⊥A1B,
由(1)知,FM∥EN,所以FM⊥A1B
又因为A1C∩A1B=A1,所以FM?⊥平面A1BC,
又因为FM 平面A1FC
平面A1FC
所以平面A1FC⊥平面A1BC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
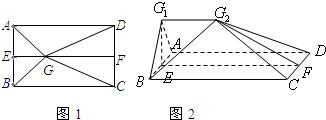 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.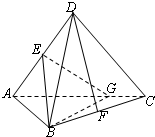 (2011•西安模拟)将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.
(2011•西安模拟)将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.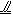
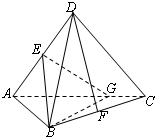 将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.
将正方形ABCD沿对角线AC折成直二面角(如图),E,F分别是AD,BC的中点.