题目内容
设数列{an}的首项a1=a≠![]() ,且
,且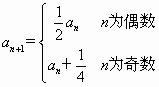 ,记
,记![]() ,n==l,2,3,….
,n==l,2,3,….
(Ⅰ)求a2,a3;
(Ⅱ)判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)求![]() .
.
答案:
解析:
解析:
|
解:(Ⅰ)a2=a1+ (Ⅱ)∵a4=a3+ 所以b1=a1- 猜想:{bn}是公比为 证明如下: 因为bn+1=a2n+1- 所以{bn}是首项为a- (Ⅲ) |

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
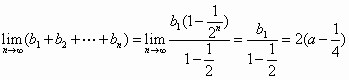 .
.