题目内容
如图,在四棱锥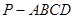 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱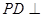 底面ABCD,
底面ABCD,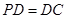 ,E是PC的中点,作
,E是PC的中点,作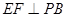 交PB于点F.
交PB于点F.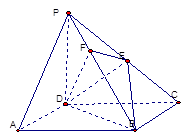
(I) 证明: PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
(1)结合线面的判定定理,根据题意得到PA∥EO是解题的关键一步
(2)根据已知的线面垂直可知PD⊥底面ABCD且DC?底面ABCD,∴PD⊥DC
,同时可知同样由PD⊥底面ABCD,得PD⊥BC.进而推理得到BC⊥平面PDC.结合判定定理得到证明。
解析试题分析:解:(1)证明:连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,∴点O是AC的中点
在△PAC中,EO是中位线,∴PA∥EO
而EO?平面EDB且PA?平面EDB,
所以,PA∥平面EDB
(2)证明:
∵PD⊥底面ABCD且DC?底面ABCD,∴PD⊥DC
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC.①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC.
而DE?平面PDC,∴BC⊥DE.②
由①和②推得DE⊥平面PBC
而PB?平面PBC,∴DE⊥PB
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD.
考点:线面垂直以及线线垂直的判定问题
点评:本小题考查直线与平面平行,直线与平面垂直,二面角等基础知识,考查空间想象能力和推理论证能力

练习册系列答案
相关题目
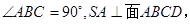


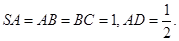
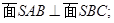
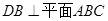 ,
,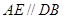 ,
,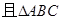 是边长为2的等边三角形,
是边长为2的等边三角形,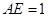 ,CD与平面ABDE所成角的正弦值为
,CD与平面ABDE所成角的正弦值为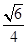 .
.
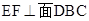 ,若存在,求线段DF的长度,若不存在,说明理由;
,若存在,求线段DF的长度,若不存在,说明理由;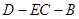 的平面角的余弦值.
的平面角的余弦值. 中,
中,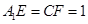 .
.
 与
与 所成角的余弦值;
所成角的余弦值; 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. BAD=90°,PA
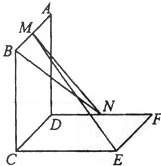
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
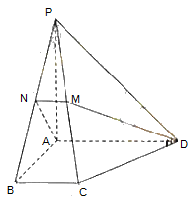

 ,底面
,底面 中
中 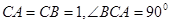 ,棱
,棱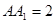 ,
,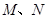 分别为
分别为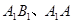 的中点.
的中点.
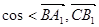 >的值;
>的值;
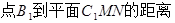 .
.