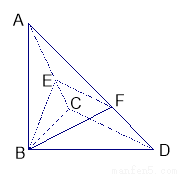
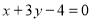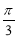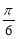题目内容
已知△ 中,
中,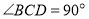 ,
,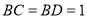 ,
, 平面
平面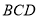 ,
,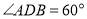 ,
,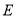 、
、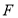 分别是
分别是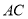 、
、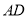 上的动点,且
上的动点,且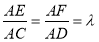
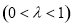 .
.
(1)求证:不论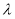 为何值,总有平面
为何值,总有平面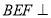 平面
平面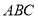 ;
;
(2)当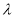 为何值时,平面
为何值时,平面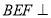 平面
平面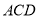 ?
?
(1)见解析;(2)见解析.
【解析】
试题分析:(1)通过证明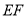 ⊥平面
⊥平面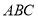 ,说明平面
,说明平面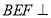 平面
平面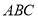 ;
;
(2)将平面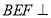 平面
平面 作为条件,利用三角形关系求解.
作为条件,利用三角形关系求解.
试题解析:(1)∵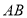 ⊥平面
⊥平面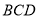 ,∴
,∴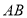 ⊥
⊥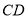 .
.
∵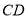 ⊥
⊥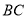 且
且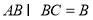 ,∴
,∴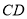 ⊥平面
⊥平面 ,
,
又∵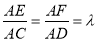
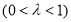 ,
,
∴不论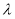 为何值,恒有
为何值,恒有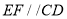 ,
,
∴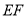 ⊥平面
⊥平面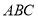 .
.
又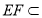 平面
平面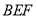 ,
,
∴不论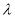 为何值,总有平面
为何值,总有平面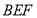 ⊥平面
⊥平面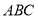 .
.
(2)由(1)知,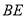 ⊥
⊥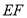 ,又平面
,又平面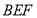 ⊥平面
⊥平面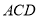 ,
,
∴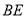 ⊥平面
⊥平面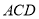 ,∴
,∴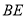 ⊥
⊥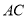 .
.
∵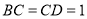 ,
,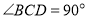 ,
,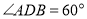 ,
,
∴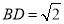 ,
,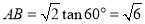 ,
,
∴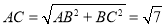 ,由
,由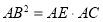 ,得
,得 ,
,
∴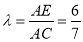 ,
,
故当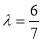 时,平面
时,平面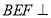 平面
平面 .
.
考点:两平面的位置关系的证明.

练习册系列答案
相关题目