题目内容
已知数列{an}中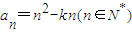 ,且{an}单调递增,则k的取值范围是( )
,且{an}单调递增,则k的取值范围是( )A.(-∞,2]
B.(-∞,3)
C.(-∞,2)
D.(-∞,3]
【答案】分析:该题需注意变量n的特殊性,根据函数的单调性可得an+1-an>0对于n∈N*恒成立,建立关系式,解之即可求出k的取值范围.
解答:解:∵数列{an}中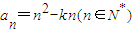 ,且{an}单调递增
,且{an}单调递增
∴an+1-an>0对于n∈N*恒成立即(n+1)2-k(n+1)-(n2-kn)=2n+1-k>0对于n∈N*恒成立
∴k<2n+1对于n∈N*恒成立,即k<3
故选B.
点评:本题主要考查了数列的性质,本题易错误地求导或把它当成二次函数来求解,注意n的取值是解题的关键,属于易错题.
解答:解:∵数列{an}中
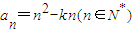 ,且{an}单调递增
,且{an}单调递增∴an+1-an>0对于n∈N*恒成立即(n+1)2-k(n+1)-(n2-kn)=2n+1-k>0对于n∈N*恒成立
∴k<2n+1对于n∈N*恒成立,即k<3
故选B.
点评:本题主要考查了数列的性质,本题易错误地求导或把它当成二次函数来求解,注意n的取值是解题的关键,属于易错题.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|