题目内容
已知双曲线C与椭圆9x2+25y2=225有相同的焦点，且离心率e=2．（1）求双曲线C的方程；
（2）若P为双曲线右支上一点，F1、F2为其焦点，且PF1⊥PF2，求△PF1F2的面积．
【答案】分析：（1）设双曲线C的方程为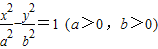
，椭圆
，由此能求出求双曲线方程．
（2）由已知条件先求出2|PF1|•|PF2|=48，由此能求出△PF1F2的面积．
解答：解：（1）设双曲线C的方程为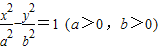
椭圆
∴
∵
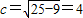
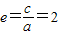∴a=2
∴b2=c2-a2=16-4=12
∴所求双曲线方程为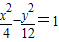
（6分）
（2）由已知得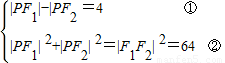
，
②-①2得2|PF1|•|PF2|=48
∴|PF1|•|PF2|=24
∴
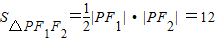（12分）
点评：本题主要考查双曲线标准方程，简单几何性质，直线与双曲线的位置关系，双曲线的简单性质等基础知识．考查运算求解能力，推理论证能力；考查化归与转化思想．综合性强，是高考的重点，易错点是双曲线的知识体系不牢固．
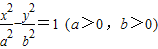，椭圆，由此能求出求双曲线方程．（2）由已知条件先求出2|PF1|•|PF2|=48，由此能求出△PF1F2的面积．
解答：解：（1）设双曲线C的方程为
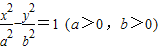
椭圆
∴
∵
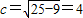
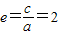∴a=2∴b2=c2-a2=16-4=12
∴所求双曲线方程为
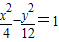（6分）（2）由已知得
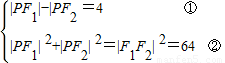，②-①2得2|PF1|•|PF2|=48
∴|PF1|•|PF2|=24
∴
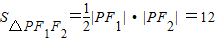（12分）点评：本题主要考查双曲线标准方程，简单几何性质，直线与双曲线的位置关系，双曲线的简单性质等基础知识．考查运算求解能力，推理论证能力；考查化归与转化思想．综合性强，是高考的重点，易错点是双曲线的知识体系不牢固．
练习册系列答案
华东师大版一课一练系列答案
相关题目
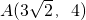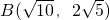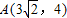，点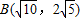
．
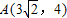，点
．
，点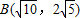
．