题目内容
(本题满分10分)已知函数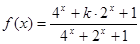 。
。
(1) 若对于任意的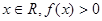 恒成立,求实数
恒成立,求实数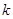 的取值范围;
的取值范围;
(2) 若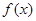 的最小值为
的最小值为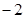 ,求实数
,求实数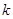 的值;
的值;
(3) 若对任意的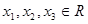 ,均存在以
,均存在以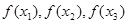 为三边长的三角形,求实数
为三边长的三角形,求实数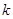 的取值范围。
的取值范围。
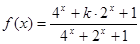 。
。(1) 若对于任意的
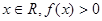 恒成立,求实数
恒成立,求实数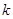 的取值范围;
的取值范围;(2) 若
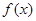 的最小值为
的最小值为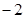 ,求实数
,求实数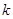 的值;
的值;(3) 若对任意的
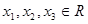 ,均存在以
,均存在以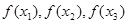 为三边长的三角形,求实数
为三边长的三角形,求实数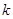 的取值范围。
的取值范围。21.(1)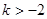
(2)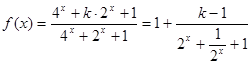 ,
,
令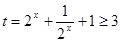 ,则
,则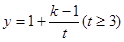 ,
,
当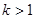 时,
时,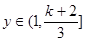 无最小值,舍去;
无最小值,舍去;
当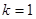 时,
时,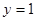 最小值不是
最小值不是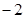 ,舍去;
,舍去;
当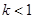 时,
时,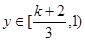 ,最小值为
,最小值为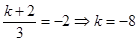 ,
,
综上所述,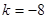 。
。
(3) 由题意,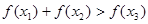 对任意
对任意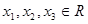 恒成立。
恒成立。
当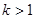 时,因
时,因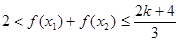 且
且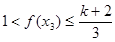 ,
,
故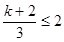 ,即
,即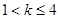 ;
;
当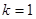 时,
时,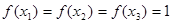 ,满足条件;
,满足条件;
当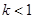 时,
时,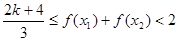 且
且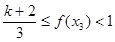 ,故
,故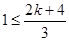 ,
,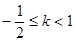 ;
;
综上所述,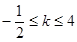
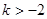
(2)
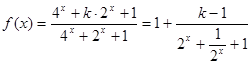 ,
,令
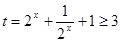 ,则
,则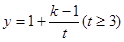 ,
,当
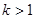 时,
时,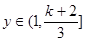 无最小值,舍去;
无最小值,舍去;当
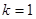 时,
时,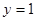 最小值不是
最小值不是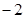 ,舍去;
,舍去;当
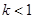 时,
时,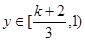 ,最小值为
,最小值为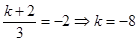 ,
,综上所述,
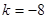 。
。(3) 由题意,
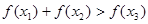 对任意
对任意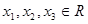 恒成立。
恒成立。当
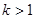 时,因
时,因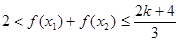 且
且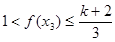 ,
,故
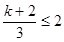 ,即
,即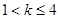 ;
;当
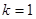 时,
时,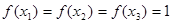 ,满足条件;
,满足条件;当
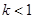 时,
时,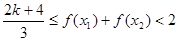 且
且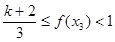 ,故
,故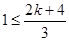 ,
,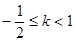 ;
;综上所述,
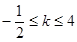
略

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
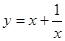
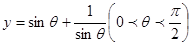
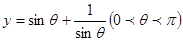
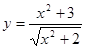
 ,据市场分析每辆客车营运的总利润
,据市场分析每辆客车营运的总利润 y(单位:万元)与营运年数x(x∈N)为二次函数关系(如图),则每辆客车营运多少年,其营运的年平均利润最大( )
y(单位:万元)与营运年数x(x∈N)为二次函数关系(如图),则每辆客车营运多少年,其营运的年平均利润最大( )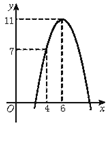

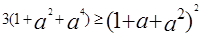 。
。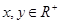 且
且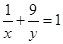 ,则
,则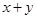 的最小值为________.
的最小值为________. 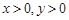 ,且
,且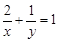 ,若
,若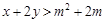 恒成立,则实数
恒成立,则实数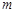 的取值范围是
的取值范围是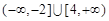
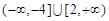
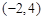
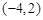
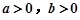 ,且满足
,且满足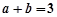 ,则
,则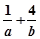 的最小值为 .
的最小值为 .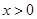 ,
,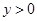 ,
,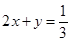 ,则
,则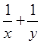 的最小值是 .
的最小值是 .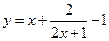 的最小值为
的最小值为