题目内容
(6分)(1) 求三次曲线 过点(2,8)的切线方程;
过点(2,8)的切线方程;
(2)求曲线 过点(0,0)的切线方程。
过点(0,0)的切线方程。
【答案】
(1) (2)
(2)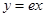
【解析】略

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
题目内容
(6分)(1) 求三次曲线 过点(2,8)的切线方程;
过点(2,8)的切线方程;
(2)求曲线 过点(0,0)的切线方程。
过点(0,0)的切线方程。
(1) (2)
(2)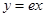
【解析】略

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案