题目内容
已知△ABC中,AC=BC=2,∠ACB=120°,D为AB的中点,E,F分别在线段AC,BC上,且EF∥AB,EF交CD于G,把△ADC沿CD折起,如图所示,
(1)求证:E1F∥平面A1BD;
(2)当二面角A1-CD-B为直二面角时,是否存在点F,使得直线A1F与平面BCD所成的角为60°,若存在求CF的长,若不存在说明理由.
【答案】分析:(1)根据同一平面内CD⊥AB且EF⊥CD,证出EF∥CD.由此可得GE1∥DA1且GF∥BD,从而得到GE1∥平面A1BD且
GF∥平面A1BD,结合面面平行判定定理得到平面E1FG∥平面A1BD,即可得到E1F∥平面A1BD;
(2)由面面垂直的判定与性质,证出A1D⊥平面BCD,得A1F在平面BCD内的射影为DF,∠A1FD就是A1F与平面BCD所成角,即∠A1FD=60°.Rt△A1FD中,由A1D=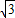 ,算出DF=1=CD,进而得到△CDF为等边三角形,可得CF=1,即存在满足条件的点F.
,算出DF=1=CD,进而得到△CDF为等边三角形,可得CF=1,即存在满足条件的点F.
解答: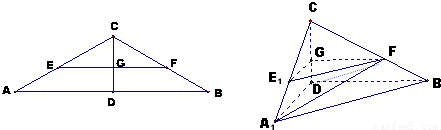 解:(1)∵AC=BC,且D为AB的中点,∴CD⊥AB,
解:(1)∵AC=BC,且D为AB的中点,∴CD⊥AB,
又∵EF∥AB,∴EF⊥CD…(2分)
在空间几何体C-A1BD中,
∵GE1∥DA1,GE1?平面A1BD,DA1?平面A1BD,∴GE1∥平面A1BD
同理可得:GF∥平面A1BD
∵GE1、GF是平面E1FG内的相交直线,
∴平面E1FG∥平面A1BD…(5分)
∵E1F?平面E1FG,∴E1F∥平面A1BD…(7分)
(2)∵二面角A1-CD-B为直二面角,∴平面A1CD⊥平面BCD
∵A1D⊥CD,平面A1CD∩平面BCD=CD,A1D?平面A1CD
∴A1D⊥平面BCD,…(9分)
可得A1F在平面BCD内的射影为DF,得∠A1FD就是A1F与平面BCD所成角,
即∠A1FD=60°…(11分)
∵Rt△A1FD中,A1D=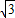 ,∴DF=1=CD
,∴DF=1=CD
∵△CDF中,∠DCF=60°,∴△CDF为等边三角形,可得CF=1.
因此,存在点F使得直线A1F与平面BCD所成的角为60°,此时CF的长为1.…(14分)
点评:本题给出平面折叠问题,求证线面平行并探索线面所成角的问题.着重考查了线面平行、面面平行的判定定理、面面垂直的性质和直线与平面所成角求法等知识,属于中档题.
GF∥平面A1BD,结合面面平行判定定理得到平面E1FG∥平面A1BD,即可得到E1F∥平面A1BD;
(2)由面面垂直的判定与性质,证出A1D⊥平面BCD,得A1F在平面BCD内的射影为DF,∠A1FD就是A1F与平面BCD所成角,即∠A1FD=60°.Rt△A1FD中,由A1D=
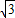 ,算出DF=1=CD,进而得到△CDF为等边三角形,可得CF=1,即存在满足条件的点F.
,算出DF=1=CD,进而得到△CDF为等边三角形,可得CF=1,即存在满足条件的点F.解答:
 解:(1)∵AC=BC,且D为AB的中点,∴CD⊥AB,
解:(1)∵AC=BC,且D为AB的中点,∴CD⊥AB,又∵EF∥AB,∴EF⊥CD…(2分)
在空间几何体C-A1BD中,
∵GE1∥DA1,GE1?平面A1BD,DA1?平面A1BD,∴GE1∥平面A1BD
同理可得:GF∥平面A1BD
∵GE1、GF是平面E1FG内的相交直线,
∴平面E1FG∥平面A1BD…(5分)
∵E1F?平面E1FG,∴E1F∥平面A1BD…(7分)
(2)∵二面角A1-CD-B为直二面角,∴平面A1CD⊥平面BCD
∵A1D⊥CD,平面A1CD∩平面BCD=CD,A1D?平面A1CD
∴A1D⊥平面BCD,…(9分)
可得A1F在平面BCD内的射影为DF,得∠A1FD就是A1F与平面BCD所成角,
即∠A1FD=60°…(11分)
∵Rt△A1FD中,A1D=
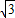 ,∴DF=1=CD
,∴DF=1=CD∵△CDF中,∠DCF=60°,∴△CDF为等边三角形,可得CF=1.
因此,存在点F使得直线A1F与平面BCD所成的角为60°,此时CF的长为1.…(14分)
点评:本题给出平面折叠问题,求证线面平行并探索线面所成角的问题.着重考查了线面平行、面面平行的判定定理、面面垂直的性质和直线与平面所成角求法等知识,属于中档题.

练习册系列答案
相关题目
