题目内容
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形ABCD的边长为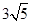 .
.

(1)求证:平面ABCD丄平面ADE;
(2)求四面体BADE的体积;
(3)试判断直线OB是否与平面CDE垂直,并请说明理由.
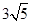 .
.
(1)求证:平面ABCD丄平面ADE;
(2)求四面体BADE的体积;
(3)试判断直线OB是否与平面CDE垂直,并请说明理由.
(1)如下(2)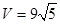 (3)OB与平面CDE不垂直
(3)OB与平面CDE不垂直
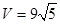 (3)OB与平面CDE不垂直
(3)OB与平面CDE不垂直试题分析:解:(1)∵AE⊥平面CDE,
 平面CDE,
平面CDE,
∴AE⊥CD,又∵正方形ABCD,∴CD⊥AD,
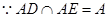 ,∴CD⊥平面ADE,
,∴CD⊥平面ADE, ,∴平面ABCD丄平面ADE.
,∴平面ABCD丄平面ADE.(2)
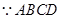 为正方形,
为正方形,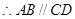 ,
,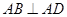 ,
,又
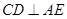 ((1)已证),
((1)已证), ,
,
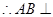 平面
平面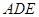 ,
,∴四面体BCDE的体积
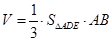 ,∵AE⊥平面CDE,∴AE⊥DE,在Rt△ADE中,
,∵AE⊥平面CDE,∴AE⊥DE,在Rt△ADE中, ,
,∴四面体ABDE的体积
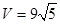 .
.(3)连结CE,由(1)知,CD⊥平面ADE,∴CD⊥DE,∴弦CE为直径,即O为CE中点.
若OB⊥平面CDE,则CD⊥CE,∴BC=BE,又AB=BC,∴AB=BE,
由(2)知,AB⊥AE,∴AB<BE,矛盾,∴OB与平面CDE不垂直.
方法2:若OB⊥平面CDE,∵AE⊥平面CDE,∴OB//AE,∴四点A、B、E、O在同一平面上,平面ABOE
 平面CDE=OE,又AB//CD,AB
平面CDE=OE,又AB//CD,AB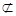 平面CDE,CD
平面CDE,CD 平面CDE,∴AB//平面CDE,∴AB//OE,∴CD//OE,矛盾.
平面CDE,∴AB//平面CDE,∴AB//OE,∴CD//OE,矛盾.点评:解决立体几何的题目,若几何体是规则的图形,则可建立空间直角坐标系,用向量去解决问题较方便。

练习册系列答案
相关题目
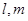 是不同的两条直线,
是不同的两条直线,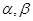 是不重合的两个平面,则下列命题中为真命题的是( )
是不重合的两个平面,则下列命题中为真命题的是( )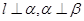 ,则
,则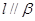
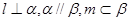 ,则
,则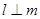
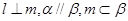 ,则
,则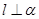
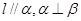 ,则
,则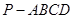 中,底面
中,底面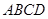 是矩形,
是矩形,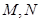 分别为
分别为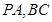 的中点,
的中点,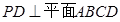 ,且
,且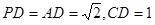
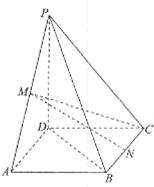
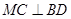 ;
;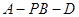 的余弦值。
的余弦值。 是边长为
是边长为 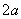 的等边三角形,
的等边三角形, 是分别以
是分别以 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿 垂直,连接
垂直,连接 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.
 ;
; 时,求三棱锥
时,求三棱锥 的体积
的体积 ;
; 的余弦值.
的余弦值. 中,
中,  ,
, ,则二面角
,则二面角 的余弦值为
的余弦值为



 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.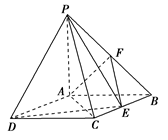
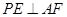 ;
;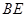 为何值时,
为何值时, 与平面
与平面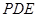 所成角的大小为45°.
所成角的大小为45°. β且α⊥β,则l⊥α
β且α⊥β,则l⊥α β=m,且l∥m, 则l∥α
β=m,且l∥m, 则l∥α 的正方体
的正方体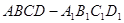 中,
中,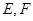 分别为
分别为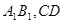 的中点.
的中点.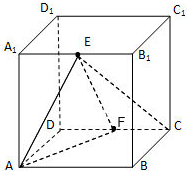
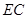 与平面
与平面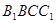 所 成 角的大小;
所 成 角的大小;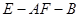 的大小.
的大小.
