题目内容
已知最小正周期为2的函数y=f（x），当x∈[-1，1]时，f（x）=x2，则函数g（x）=f（x）-|log5x|的零点个数为（ ）
分析：先根据函数的周期性画出函数y=f（x）的图象，以及y=|log5x|的图象，结合图象当x＞5时，y=|log5x|＞1此时与函数y=f（x）无交点，即可判定函数g（x）=f（x）-|log5x|的零点个数．
解答：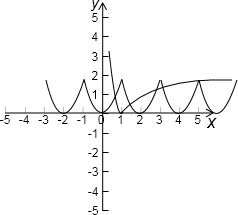
解：根据周期性画出函数y=f（x）的图象，
y=|log5x|的图象，
根据y=|log5x|在（1，+∞）上单调递增函数，当x=5时|log55|=1，
∴当x＞5时y=|log5x|＞1此时与函数y=f（x）无交点，
结合图象可知有5个交点，
则函数g（x）=f（x）-|log5x|的零点个数为5，
故选C．
解：根据周期性画出函数y=f（x）的图象，y=|log5x|的图象，
根据y=|log5x|在（1，+∞）上单调递增函数，当x=5时|log55|=1，
∴当x＞5时y=|log5x|＞1此时与函数y=f（x）无交点，
结合图象可知有5个交点，
则函数g（x）=f（x）-|log5x|的零点个数为5，
故选C．
点评：本题考查函数的零点，求解本题，关键是研究出函数f（x）性质，作出其图象，将函数y=f（x）-|log5x|的零点个数的问题转化为两个函数交点个数问题是本题中的一个亮点，此一转化使得本题的求解变得较容易．
练习册系列答案
相关题目