题目内容
9、已知最小正周期为2的函数y=f(x),当x∈[-1,1]时,f(x)=x2,则函数y=f(x)(x∈R) 的图象与y=|log5x|的图象的交点个数为
5
.分析:先根据函数的周期性画出函数y=f(x)的图象,以及y=|log5x|的图象,结合图象当x>5时,y=|log5x|>1此时与函数y=f(x)无交点,即可判定交点的个数.
解答: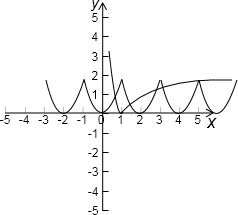 解:根据周期性画出函数y=f(x)与y=|log5x|的图象,
解:根据周期性画出函数y=f(x)与y=|log5x|的图象,
根据y=|log5x|在(1,+∞)上单调递增函数,当x=5时|log55|=1,
∴当x>5时y=|log5x|>1此时与函数y=f(x)无交点,
结合图象可知有5个交点,
故答案为:5.
 解:根据周期性画出函数y=f(x)与y=|log5x|的图象,
解:根据周期性画出函数y=f(x)与y=|log5x|的图象,根据y=|log5x|在(1,+∞)上单调递增函数,当x=5时|log55|=1,
∴当x>5时y=|log5x|>1此时与函数y=f(x)无交点,
结合图象可知有5个交点,
故答案为:5.
点评:本题主要考查了周期函数与对数函数的图象,数形结合是高考中常用的方法,我们本着能画图就画图的原则,本题属于基础题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目