题目内容
已知直线l:mx+ny-1=0(m,n∈R*)与x轴相交于点A,与y轴相交于点B,且直线l与圆x2+y2=4相交所得弦长为2.
(Ⅰ)求出m与n的关系式;
(Ⅱ)若直线l与直线2x+y+5=0平行,求直线l的方程;
(Ⅲ)若点P是可行域
内的一个点,是否存在实数m,n使得|OA|+|OB|的最小值为2
,且直线l经过点P?若存在,求出m,n的值;若不存在,说明理由.
(Ⅰ)求出m与n的关系式;
(Ⅱ)若直线l与直线2x+y+5=0平行,求直线l的方程;
(Ⅲ)若点P是可行域
|
| 6 |
分析:(I)由圆的方程找出圆心坐标和半径r,由直线l被圆截得的弦长与半径,根据垂径定理及勾股定理求出圆心到直线l的距离,然后再利用点到直线的距离公式表示出圆心到直线l的距离,两者相等列出关系式,整理后求出m2+n2的值,
(II)根据直线平行的条件求出m=2n,再代入(I)求得式子,即可求得所求的直线的方程.
(III)对于存在性问题,可先假设存在,即假设存在实数m,n使得|OA|+|OB|的最小值为2
,且直线l经过点P.再利用线性规划的方法,研究取得最值的条件,若出现矛盾,则说明假设不成立,即不存在;否则存在.
(II)根据直线平行的条件求出m=2n,再代入(I)求得式子,即可求得所求的直线的方程.
(III)对于存在性问题,可先假设存在,即假设存在实数m,n使得|OA|+|OB|的最小值为2
| 6 |
解答:解:(I)由圆x2+y2=4的方程,得到圆心坐标为(0,0),半径r=2,
∵直线l与圆x2+y2=4相交所得弦CD=2,
∴圆心到直线l的距离d═
=
,
∴圆心到直线l:mx+ny-1=0的距离d═
=
,
整理得:m2+n2=
,
(II)直线l:mx+ny-1=0的斜率为-
,直线2x+y+5=0的斜率为-2,∴-
=-2,m=2n
结合(I)得m=
,n=
,
故所求的直线的方程为 2x+y-
=0,
 (III)令直线l解析式中y=0,解得:x=
(III)令直线l解析式中y=0,解得:x=
,
∴A(
,0),即OA=
,
令x=0,解得:y=
,∴B(0,
),即OB=
,
则OA+OB=
+
≥2
≥2
,当且仅当m=n=
时,OA+OB取最小值.此时直线l的方程为:
x+y-
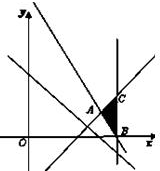
=0,如图,作出可行域
的图形,是一个三角形ABC及其内部,而△ABC及其内部
都在直线x+y-
=0的同侧,与直线x+y-
=0没有公共点,
所以不存在满足条件的直线l,即不存在实数m,n使得|OA|+|OB|的最小值为2
,且直线l经过点P.
∵直线l与圆x2+y2=4相交所得弦CD=2,
∴圆心到直线l的距离d═
r2-(
|
| 3 |
∴圆心到直线l:mx+ny-1=0的距离d═
| 1 | ||
|
| 3 |
整理得:m2+n2=
| 1 |
| 3 |
(II)直线l:mx+ny-1=0的斜率为-
| m |
| n |
| m |
| n |
结合(I)得m=
2
| ||
| 15 |
| ||
| 15 |
故所求的直线的方程为 2x+y-
| 15 |
 (III)令直线l解析式中y=0,解得:x=
(III)令直线l解析式中y=0,解得:x=| 1 |
| m |
∴A(
| 1 |
| m |
| 1 |
| m |
令x=0,解得:y=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
则OA+OB=
| 1 |
| m |
| 1 |
| n |
|
| 6 |
| ||
| 6 |
x+y-
| 6 |
|
都在直线x+y-
| 6 |
| 6 |
所以不存在满足条件的直线l,即不存在实数m,n使得|OA|+|OB|的最小值为2
| 6 |
点评:本小题主要考查点到直线的距离公式、直线的一般式方程与直线的平行关系、简单线性规划等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xoy中,已知“葫芦”曲线C由圆弧C1与圆弧C2相接而成,两相接点M,N均在直线y=-
如图,在平面直角坐标系xoy中,已知“葫芦”曲线C由圆弧C1与圆弧C2相接而成,两相接点M,N均在直线y=- 内的一个点,是否存在实数m,n使得|OA|+|OB|的最小值为2
内的一个点,是否存在实数m,n使得|OA|+|OB|的最小值为2 ,且直线l经过点P?若存在,求出m,n的值;若不存在,说明理由.
,且直线l经过点P?若存在,求出m,n的值;若不存在,说明理由. 上.圆弧C1所在圆的圆心是坐标原点O,半径为r1=2;圆弧C2过点A(0,-6
上.圆弧C1所在圆的圆心是坐标原点O,半径为r1=2;圆弧C2过点A(0,-6 ).
). =0与“葫芦”曲线C交于E,F两点.当|EF|=4+4
=0与“葫芦”曲线C交于E,F两点.当|EF|=4+4 时,求直线l的方程.
时,求直线l的方程.