题目内容
(14分)如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,椭圆以
,椭圆以![]() 、
、![]() 为焦点且经过点
为焦点且经过点![]() .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)若点![]() 满足
满足![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() ?若存在,求出直线
?若存在,求出直线 ![]() 与
与![]() 夹角
夹角![]() 的正切值的取值范围;若不存在,请说明理由.
的正切值的取值范围;若不存在,请说明理由.

解析:(Ⅰ)如图,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立直角坐标系
轴建立直角坐标系
则![]() ,
,![]() ,
,![]() ,
,![]() ………2分
………2分
设椭圆方程为![]()
则
解得 ………………4分
………………4分
∴所求椭圆方程为![]() …………………5分
…………………5分

(Ⅱ)由![]() 得点
得点![]() 的坐标为
的坐标为![]()
显然直线 ![]() 与
与![]() 轴平行时满足题意,即
轴平行时满足题意,即![]() …………6分
…………6分
直线 ![]() 与
与![]() 轴垂直时不满足题意
轴垂直时不满足题意
不妨设直线 ![]() ……………7分
……………7分
由 得
得 ![]() ………9分
………9分
由 ![]() 得
得 ![]() ………10分
………10分
设![]() ,
,![]() ,
,![]() 的中点为
的中点为![]()
则![]() ,
,![]() ………11分
………11分
∵![]()
∴![]()
∴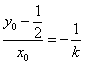 即
即 
解得:![]() ………………12分
………………12分
由  得
得 ![]() 且
且 ![]() …………13分
…………13分
故直线 ![]() 与
与![]() 夹角
夹角![]() 的正切值的取值范围是
的正切值的取值范围是![]() ……………14分
……………14分

练习册系列答案
相关题目

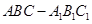 中,
中, ,
, ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.  平面
平面 ;
;  平面
平面 ;
;
 中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
 中,
中, ,点
,点 在边
在边 上,
上, 。
。 平面
平面 ;
; 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.