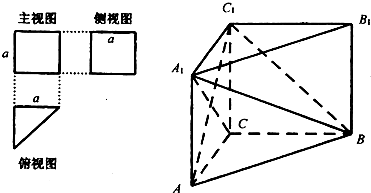
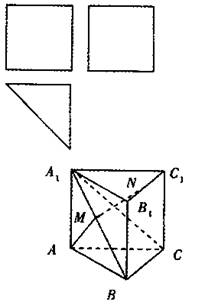
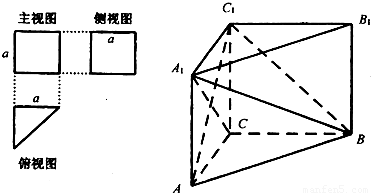
题目内容
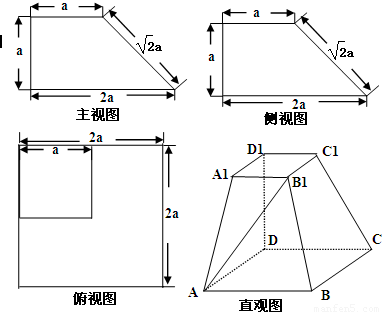
一个多面体的三视图及直观图如图所示:(Ⅰ)求异面直线AB1与DD1所成角的余弦值:
(Ⅱ)试在平面ADD1A1中确定一个点F,使得FB1⊥平面BCC1B1;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-CC1-B的余弦值.
【答案】分析:(I)建立空间直角坐标系,设AB=2A1B1=2DD1=2a,求出 =(-a,a,a),
=(-a,a,a), =(0,0,a),利用向量的夹角公式,可得结论;
=(0,0,a),利用向量的夹角公式,可得结论;
(II)由FB1⊥平面BCC1B1,利用向量的数量积公式,即可得出结论;
(III)确定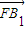 为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.
为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.
解答: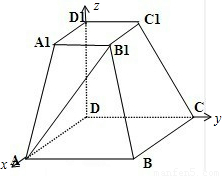 解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分)
解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分)
以D为原点,DA、DC、DD1所在的直线为x,y,z轴,
建立如图所示的空间直角坐标系,则D(0,0,0),A(2a,0,0),B1(a,a,a),D1(0,0,a),B(2a,2a,0),C(0,2a,0),C1(0,a,a)…(4分)
(Ⅰ)∵ =(-a,a,a),
=(-a,a,a), =(0,0,a)
=(0,0,a)
∴cos< >=
>= =
=
即直线AB1与DD1所成角的余弦值为 …(6分)
…(6分)
(II)设F(x,0,z),∵ =(-a,a,a),
=(-a,a,a), =(-2a,0,0),
=(-2a,0,0), =(a-x,a,a-z)
=(a-x,a,a-z)
由FB1⊥平面BCC1B1得
即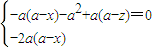 得
得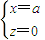
∴F(a,0,0)即F为DA的中点…(9分)
(III)由(II)知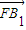 为平面BCC1B1的法向量.
为平面BCC1B1的法向量.
设 =(x1,y1,z,)为平面FCC1的法向量.
=(x1,y1,z,)为平面FCC1的法向量.
∵ =(0,-a,a),
=(0,-a,a), =)-a,2a,0)
=)-a,2a,0)
∴
令y1=1得x1=2,z1=1
∴ =(2,1,1)
=(2,1,1)
∴cos< >=
>=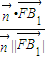 =
=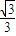
即二面角F-CC1-B的余弦值为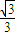 …(12分)
…(12分)
点评:本题考查线面垂直,考查空间角,考查向量知识的运用,考查学生的计算能力,属于中档题.
 =(-a,a,a),
=(-a,a,a), =(0,0,a),利用向量的夹角公式,可得结论;
=(0,0,a),利用向量的夹角公式,可得结论;(II)由FB1⊥平面BCC1B1,利用向量的数量积公式,即可得出结论;
(III)确定
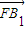 为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.
为平面BCC1B1的法向量,求出平面FCC1的法向量,利用向量的夹角公式,可得结论.解答:
 解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分)
解;依题意知,该多面体为底面是正方形的四棱台,且D1D⊥底面ABCD,AB=2A1B1=2DD1=2a…(2分)以D为原点,DA、DC、DD1所在的直线为x,y,z轴,
建立如图所示的空间直角坐标系,则D(0,0,0),A(2a,0,0),B1(a,a,a),D1(0,0,a),B(2a,2a,0),C(0,2a,0),C1(0,a,a)…(4分)
(Ⅰ)∵
 =(-a,a,a),
=(-a,a,a), =(0,0,a)
=(0,0,a)∴cos<
 >=
>= =
=
即直线AB1与DD1所成角的余弦值为
 …(6分)
…(6分)(II)设F(x,0,z),∵
 =(-a,a,a),
=(-a,a,a), =(-2a,0,0),
=(-2a,0,0), =(a-x,a,a-z)
=(a-x,a,a-z)由FB1⊥平面BCC1B1得
即
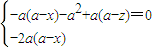 得
得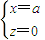
∴F(a,0,0)即F为DA的中点…(9分)
(III)由(II)知
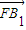 为平面BCC1B1的法向量.
为平面BCC1B1的法向量.设
 =(x1,y1,z,)为平面FCC1的法向量.
=(x1,y1,z,)为平面FCC1的法向量.∵
 =(0,-a,a),
=(0,-a,a), =)-a,2a,0)
=)-a,2a,0)∴

令y1=1得x1=2,z1=1
∴
 =(2,1,1)
=(2,1,1)∴cos<
 >=
>=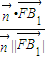 =
=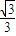
即二面角F-CC1-B的余弦值为
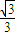 …(12分)
…(12分)点评:本题考查线面垂直,考查空间角,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目